After a survey of inverse transform methods for the efficient
synthesis of narrow-band and broad-band signals a novel spectral
line broadening technique is introduced for synthesis of pitch
modulated noise signals. A real-time sound synthesizer integrating
these methods is described and its application in musical sound
spatialization is explained.
The term "noise" is used to describe the perception
of a multitude of features of sounds from musical instruments,
for example:
The Sum of Sinusoid+Residual models of McAulay/Quatieri, Serra/Smith, Depalle/Rodet, etc., have proved useful for modeling and coding short musical tones. The assumption of these models is that the residual is colored independently of sinusoidal parameter estimates. This assumption is invalid for most musical instruments so inadequate fusion of re-synthesized noise and sinusoidal components is often observed. This is especially troublesome when transformations are applied such as time scaling and pitch shifting [1-3].
The problem is that all forced oscillators (bowed strings, voice, reeds, trumpets, flue pipes, etc.) generate nearly-periodically modulated noise not additive noise. A combination of a better understanding of the physics of these oscillatory mechanisms [4, 5] and new methods in higher order statistics [6, 7], wavelets [8] and time series [9] are leading to better tools for multi-level decomposition of sounds into transient events, pitched and unpitched oscillations, convolutional noise and colored noise. These new models require efficient, real-time noise synthesis algorithms, the main focus of this paper.
The paper is structured as follows. Section one reviews transform-domain sound synthesis implementations and noise modeling methods. Section two describes the architecture of an additive synthesizer and related components that constitute CNMAT s additive synthesis tools (CAST). Section three describes in more detail how noise is controlled and synthesized in CAST. Section four introduces the flexible output routing architecture of the synthesizer and its applications in spatial aspects of sound reproduction.
The idea of synthesizing sounds by summing sinusoids [10] has intrigued generations of musical instrument builders, audio engineers and thinkers. Thaddeus Cahill's electromechanical implementations of the late 1800 s [11] illustrate graphically the basic challenge faced by these engineerscthe creation of a large number of oscillators with accurate frequency control. Cahill used dynamos constructed from wheels of different sizes attached to rotating shafts ranging in length from 6 to 30 feet. The speed of each shaft was adjusted to obtain the required pitch. A total of 145 alternators were attached to the shafts. Since the vacuum tube and transistor (inventions of this century) were unavailable to Cahill, each rotating element had to produce nearly 12000 to 15000 watts of energy to deliver synthesized music to subscribers' homes.
In the late 1970's, the availability of single chip digital multipliers stimulated the construction of digital signal processors for musical applications [12]. Although these machines were capable of accurately synthesizing hundreds of sinusoids [13], their prohibitive cost and limited programming tools prevented widespread use. A new signal synthesis method was needed that could better exploit the rapid advances in integrated circuit integration and computer architecture.
Since sinusoidal summation models involve spectral descriptions, the key to an efficient new algorithm for additive synthesis is an efficient transformation from frequency to signal domain. Although the Fast Fourier Transform (FFT) was widely known and used since its rediscovery and introduction in 1965 [14], the challenges to its use for continuous synthesis of multiple sinusoids were not surmounted until the 1970 s. The inverse FFT was used in 1973 for simulations of seismograms [15]. In a 1974 thesis, R.H. Davis [16] pioneered the two essential features of a synthesis window and overlap-add process. Unfortunately, this doctoral thesis work was not widely known and is not cited in the first paper to introduce a complete theory for the weighted overlap-add method of short-time Fourier analysis/synthesis [17] that forms the basis for all subsequent transform domain additive synthesis algorithms. This theory was developed from a line of work motivated by applications in speech coding and processing including Shafer and Rabiner s use of the FFT in a speech analysis/synthesis system [18], Allen s exposition of the overlap-add synthesis method [19], and Portnoff s use of distinct analysis and synthesis windows [20, 21].
The first musical application of the weighted overlap-add inverse FFT method is described in a book by Chamberlin [22]. The benefits of the method are not obvious from this exposition because of the poor performance of the triangular and sine-squared windows suggested and a lack of affordable computers for the FFT calculations.
The next important development came again from the speech research community with the introduction of sinusoidal models for speech coding [23]. The inverse FFT method was applied to synthesize sinusoidally coded speech in 1988 [24]. In 1992 George and Smith described a musical tone synthesis scheme using the inverse FFT [25].
An important result of the work pioneered in speech by Almeida and Silva [26] and on music signals by Serra and Smith [27-29] was the development of analysis methods that decompose signals into a set of sinusoidal components and a "noisy" residual. Both these teams suggested the use of the inverse FFT to efficiently synthesize the noisy residual, but the history of the use of the FFT for the synthesis of random signals began much earlier. Inspired by a suggestion from Einstein in 1915 [30], Lanczos and Gellai [31] study random sequences using Fourier analysis. As early as 1973 Wittig and Sinha [32, 33] applied the inverse FFT for the synthesis of multicorrelated random processes. In 1973 Smith [34] uses the inverse FFT to synthesize a random radio frequency signal with a specific spectral shape and in 1975 Nakamura et al. [35] used Fourier synthesis for a dielectric spectrometer. In 1978 Lemke and Richter generated random sequences for simulation experiments using the inverse FFT [36]. Holmes [37] simulated wind records with the inverse FFT in 1978 also. The first appearance of the overlap-add technique to smoothly generate continuous random sequences may again have been Davis [16]. The 1979 journal paper [38] describes the same technique but appears to have been developed independently of Davis.
By the early 1980 s the theory of transform domain synthesis of sinusoids and noise was well developed and had been applied in speech, music and other applications. More widespread application of this theory would require algorithms that efficiently exploited available computing machinery. In 1987 Rodet et al. developed tools for musical signal processing on an array coprocessor attached to a Sun workstation [39]. FFT s are efficiently implemented on array processors so Depalle and Rodet [40] developed an additive synthesizer based on the Inverse FFT for their musical workstation. This was the first real-time transform domain music synthesizer. By the early 1990 s workstations and desktop computers were fast enough for real-time implementations of additive synthesis with hundreds of partials [41].
The expedient of using the same inverse transform for synthesis of both sinusoidal partials and noise was known by McAualay and Quatieri in 1988 [42] and implemented by this author for reactive, real-time musical applications [43]. Unfortunately this offers no particular advantage over subtractive techniques, e.g., lattice filtered white noise [27] without an efficient, low dimensional control structure for the spectral envelope of the noise. Marques [44] proposed a scheme using narrow band basis functions. Carl [45] developed this idea using basis functions chosen according to critical bands equispaced on a Bark scale. Goodwin [46] created an analysis tool using this technique for fixed frequency bands. This author [47] developed an efficient real-time implementation of noise synthesis by frequency bands and an associated control structure supporting time scaling and timbral interpolation [48, 49].
Modulating the phase of a sinusoidal carrier with a random signal results in a narrow band noise source. This spectral broadening process has been used for decades in spread spectrum RF communications systems where it is implemented directly in the time domain. Musical applications of line broadening were explored by Risset and Wessel in the 1970 s [50]. Implementations of this idea in the transform domain require a frequency domain description of a modulated sinusoid. The analysis side of this problem was addressed by Marques and Almeida [51, 52]. Tabei and Ueda [53] explore the synthesis issues and Goodwin [54] sought efficient algorithms for non-stationary sinusoids [55, 56]. Unfortunately the key optimizations that make sinusoidal synthesis so efficient in the transform domain depend on the narrow band property of a constant frequency sine wave. This author developed a novel compromise [43] for synchronous noise synthesis by adding random values to the phases of transform values for each bin in the transform associated with each sinusoid. The control structure and implementation of this method will be described in detail in later sections.
Although spectral line broadening may be implemented in time-domain additive synthesizers [57], no provision for it has been made to date in custom VLSI real-time systems [58-60]. One reason for this is that the interface between the musical control software and the synthesis circuits is the primary performance bottleneck and increasing the number of parameters across the interface worsens the problem. Transform domain methods avoid this bottleneck by computing the control and synthesis functions in a single address space and by computing control functions at a frame rate, typically around 1/100th of the output sample rate.
Concluding this survey, one hundred years of rapid gains in computational accuracy and performance since Cahill's electromechanical additive synthesizer have resulted in systems capable of real-time control of thousands of line broadened sinusoidal partials and spectrally shaped noise on desktop computers.
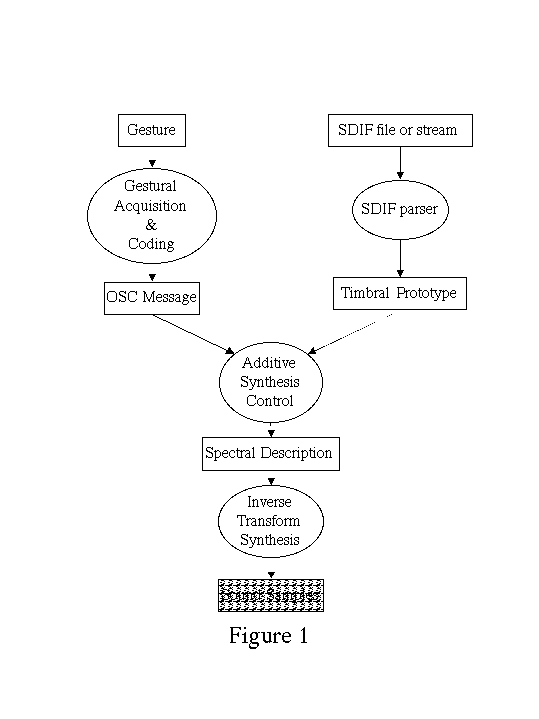
CNMAT s Additive Synthesis tools consist of a real-time additive synthesizer server, control clients such as a timbral prototype editor [61, 62], and sound analysis and modeling programs. Figure 1 and subsequent figures use the convention that rectangular objects encapsulate data, round objects encapsulate process. Synthesis clients communicate with the additive synthesizer using OpenSound Control (OSC), an open, efficient, transport-independent, message-based protocol developed for communication among computers, sound synthesizers, and other multimedia devices [63]. Analysed sounds and timbral models are represented using the Sound Description Interchange Format (SDIF)[64].

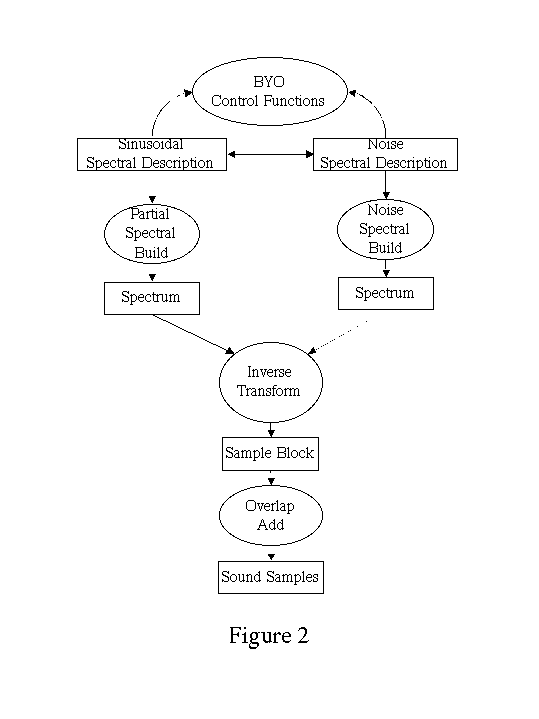
The CAST synthesizer (Figure 2) was designed to exploit a major advantage of additive synthesis c the ability to integrate a wide range of sound models. Of particular importance is the formal and implemented distinction between computations on models of sounds (the control structure) and the final conversion of the resulting spectral description into an audio sample stream (additive synthesis). The "BYO plug-in" programming mechanism supports flexible control structures [65] and the real-time implementation issues [41] have been described elsewhere. The rest of this paper will focus on the spectral description and synthesis aspects of CAST.
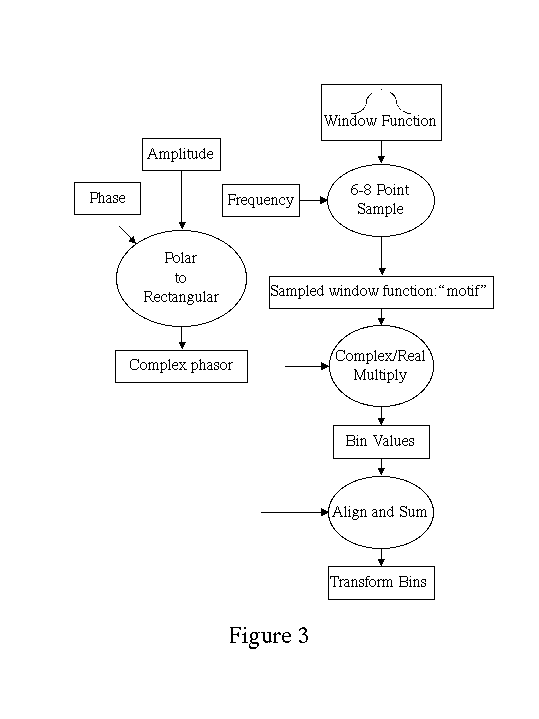
The computational kernel of transform domain sinusoidal synthesis is illustrated in Figure 3. A very efficient inner loop iterates over each sinusoid in the set of partials. The inner loop length is minimized by exploiting a transform (e.g., Fourier) that localizes the energy of constant frequency, constant amplitude sinusoids. By careful choice of synthesis window and transform the number of spectral bins computed for each sinusoid can be reduced to around six with minimal audible artifacts. The inner loop samples the spectral transform of the synthesis window to yield a scale factor for each bin value. The bin values are computed by projection of the vector of the desired phase and amplitude. This polar to rectangular conversion is performed outside the inner loop, typically using tables for the sine and cosine calculation. The inner loop is thus reduced to a short sequence of real/complex multiplications and complex additions. The good match of this computational structure to the external/secondary-cache/primary-cache/register memory hierarchy of modern computers is the reason transform methods can outperform direct oscillator implementations. The dozen or so instructions for the inner loop result in an entire frame of roughly a hundred samples of sound output.
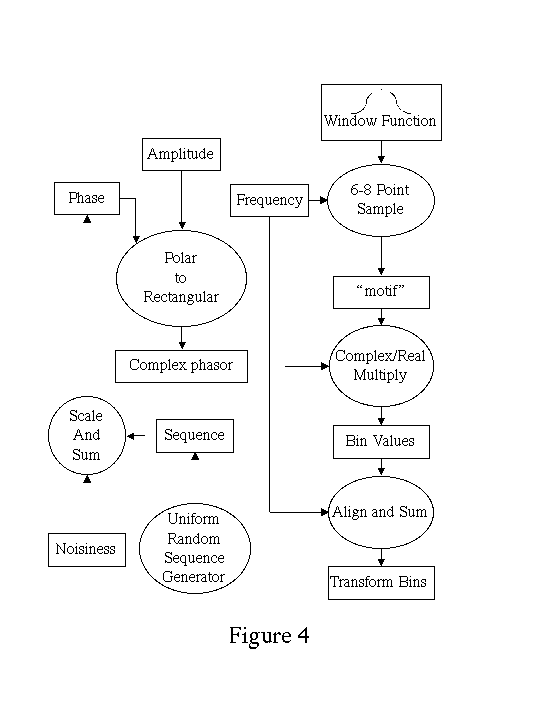
Spectral line broadening may be introduced into the sinusoidal synthesis kernel by modulating the phase of the sinusoid by a scaled, zero-meaned, uniform random value (Figure 4). This additional computation is performed outside the inner loop and since the random sequence can be tabulated, the additional cost for spectral line broadening is smallc significantly smaller than the analogous computation for oscillator methods.
With appropriate parameters for the noise amplitudes, sounds synthesized using this spectral line broadening process are perceived as similar to the noise found in voice and musical instruments such as flutes and flue pipes. Since the two noise generating mechanisms are quite different, it is interesting to consider what features the mechanisms have in common that may explain a similar percept. In the voice and instruments mentioned above, the noise process is the result of turbulence, the amplitude of which is dependent on air velocity which is modulated by the nearly periodic primary oscillator. The fundamental frequency and partial amplitudes are not greatly influenced by the turbulence. This independence is a feature of the spectral line broadening process because of the use of a zero mean random phase modulation.
In physical systems the amplitude of the primary oscillator and turbulent noise are both proportional to driving energy. The amplitude parameter of the line broadening spectral synthesis process conveniently adjusts the amplitude of both elements. This parameterization is a convenient starting point for more sophisticated musical instrument models that dose noise and partial energy according to frequency and driving force.
In musical instruments it is common for the peaks of the noise spectrum to be close in frequency to the harmonics of the fundamental frequency of a primary oscillator because of the influence of the same passive resonator on both sources. This situation is very compactly simulated by simply broadening the spectral lines for each partial used for the primary oscillator. However, this may not model high frequency partials correctly because the passive modes of musical instrument resonators are often inharmonic. Phase locking from a non-linear process ties the partials of the primary oscillator to a harmonic relationship. Noise processes are spectrally shaped according to passive modes. This effect is described by Verge for flue pipes [66-68] and can be expected for bowed strings also. In the voice the primary oscillator and noise generating mechanisms are often not coupled to the same resonators at all. This can be heard by comparing an attempt to communicate a phrase using turbulence from the glottis (i.e., whispering), and turbulent sources from the locations that create the fricatives and plosives, e.g., the k, t, s and f sounds. In these cases, successful synthesis is achieved by adding narrow band sources at frequencies different from the partial frequencies of the primary oscillator.
A final important connection between sounds created by spectral line broadening and modulated noise is that both are perceived as originating from a single source. In contrast to additive noise models, the integrity of spectral line broadened sources survives musically useful transformations such as transposition, and time dilation and compression.
Figure 5 illustrates how the computational kernel of transform domain additive synthesis may be extended to distribute energy from each sinusoidal partial to two independent spectra. Careful implementation of this extended kernel is more efficient than the alternative of separate synthesis of partials for each output. An interesting application of this multi-spectral synthesis kernel is to create sound sources with frequency-dependent directivity using arrays of loudspeakers driven by separate signal streams derived from each spectra [69-73].
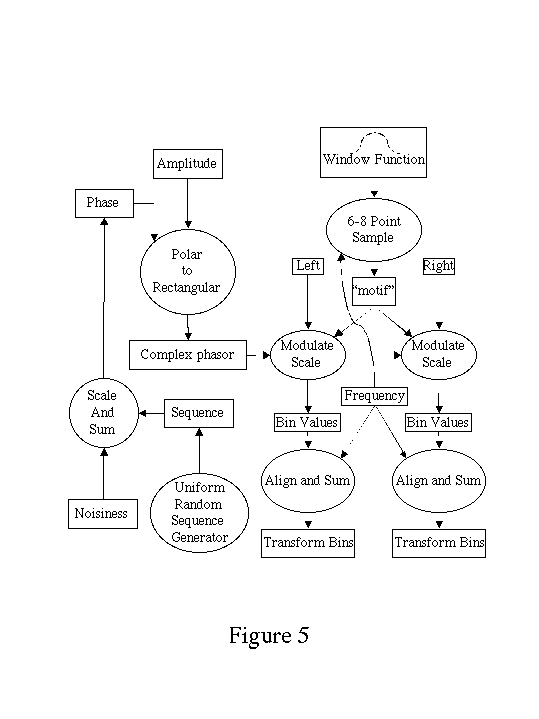
Source decorrelation is an important process used in spatialization applications [74, 75] and may be efficiently achieved by manipulation of the phases of partials as they are summed into output spectra.
The aformentioned extensions of transform domain methods from sinusoids to noise signals will enable broader application of additive sound synthesis in speech and music.
The author thanks Dr. Puritz, for his introduction to the mathematics of computation of the elementary functions;
Xavier Rodet for patiently explaining transform domain synthesis;
David Wessel for sharing his wealth of experience with musical applications of additive synthesis;
Gibson Guitar Inc. for financial support of this research.
1. Laroche, J., Y. Stylianou, and E. Moulines. HNS: Speech modification based on a harmonic+noise model. Proceedings of the 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing (Cat. No.92CH3252-4) Proceedings of ICASSP '93. 1993. Minneapolis, MN, USA: IEEE.
2. Laroche, J. and M. Dolson. Phase-vocoder: about this phasiness business. Proceedings of the ASSP Workshop on Applications of Signal Processing to Audio and Acoustics. 1997. New Paltz, NY: IEEE.
3. Laroche, J. Autocorrelation method for high-quality time/pitch-scaling. Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. 1993. New York: IEEE.
4. Rodet, X., Models of musical instruments from Chua's circuit with time delay. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 1993. 40(10): p. 696-701.
5. Rodet, X. One and two mass Models of Oscillations for Voice and Instruments. Proceedings of the Inernational Computer Music Conference. 1995. Banff, Canada: CMA.
6. Dubnov, S. and X. Rodet. Statistical Modeling of Sound Aperiodicities. Proceedings of the International Computer Music Conference. 1997. Thessaloniki, Greece: CMA.
7. Brillinger, D.R. and R.A. Irizarry, An investigation of the second- and higher-order spectra of music. Signal Processing, 1998. 65(2): p. 161-179.
8. Goodwin, M. and M. Vetterli. Time-frequency signal models for music analysis, transformation, and synthesis. Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis. 1996. Paris, France: IEEE.
9. Irizarry, R., Statistics and Music: Fitting a Local Harmonic Model to Musical Sound Signals, 1998, Ph. D. Thesis, UC Berkeley.
10. Helmholtz, H.v. and A.J. Ellis, On the sensations of tone as a physiological basis for the theory of music. 1875, New York,: Dover Publications. 576.
11. Nicholl, M., Good Vibrations, in Invention and Technology. 1993.
12. Allen, J., Computer architecture for digital signal processing. Proceedings of the IEEE, 1985. 73(5): p. 852-73.
13. DiGiugno, G. A 256 Digital Oscillator Bank. Proceedings of the Computer Music Conference. 1976. Cambridge, Massachusetts: M.I.T.
14. Cooley, J.W. and J.W. Tukey, An algorithm for the machine computation of complex Fourier Series. Mathematics of Computation, 1965. 19: p. 297-301.
15. Knopoff, L., F. Schwab, and E. Kausel, Interpretation of Lg. Geophysical Journal of the Royal Astronomical Society, 1973. 33(4): p. 389-404.
16. Davis, R.H., Synthesis of steady-state signal components by an all-digital system, 1974, Ph. D. Thesis, Maryland.
17. Crochiere, R.E., A weighted overlap-add method of short-time Fourier analysis/synthesis. IEEE Transactions on Acoustics, Speech and Signal Processing, 1980. ASSP-28(1): p. 99-102.
18. Schafer, R.W. and L.R. Rabiner, Design and simulation of a speech analysis-synthesis system based on short-time Fourier analysis. IEEE Transactions on Audio and Electroacoustics, 1973. AU-21(3): p. 165-74.
19. Allen, J.B. and L.R. Rabiner, A unified approach to short-time Fourier analysis and synthesis. Proceedings of the IEEE, 1977. 65(11): p. 1558-64.
20. Portnoff, M.R., Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Transactions on Acoustics, Speech and Signal Processing, 1980. ASSP-28(1): p. 55-69.
21. Portnoff, M.R., Implementation of the digital phase vocoder using the fast Fourier transform. IEEE Transactions on Acoustics, Speech and Signal Processing, 1976. ASSP-24(3): p. 243-8.
22. Chamberlin, H., Musical applications of microprocessors. The Hayden microcomputer series. 1980, Rochelle Park, N.J.: Hayden Book Co. 661.
23. McAulay, R.J. and T.F. Quatieri. Mid-rate coding based on a sinusoidal representation of speech. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. 1985. Tampa, FL, USA: IEEE.
24. McAulay, R.J. and T.F. Quatieri. Computationally efficient sine-wave synthesis and its application to sinusoidal transform coding. Proceedings of the ICASSP. 1988. New York, NY, USA: IEEE.
25. George, E.B. and M.J.T. Smith, Analysis-by-synthesis/overlap-add sinusoidal modeling applied to the analysis and synthesis of musical tones. Journal of the Audio Engineering Society, 1992. 40(6): p. 497-516.
26. Almeida, L.B. and F.M. Silva. Variable-frequency synthesis: an improved harmonic coding scheme. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing. 1984. San Diego, CA: IEEE.
27. Serra, X., A System for Sound Analys/Transformation/Synthesis Based ona Deterministic Plus Stochastic Decomposition, 1989, PhD Thesis, Stanford.
28. Serra, X. and J.O. Smith. A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition. Proceedings of the Fifth European Signal Processing Conference EUSIPCO-90. 1990. Barcelona, Spain: Elsevier.
29. Serra, X. and J. Smith, III, Spectral modeling synthesis: a sound analysis/synthesis system based on a deterministic plus stochastic decomposition. Computer Music Journal, 1990. 14(4): p. 12-24.
30. Einstein, A., Antwort auf eine Abhandlung M. v. Laues "Ein Satz der Wahrscheinlichkeitsrechnung und seine Anwendung auf die Strahlungstheorie". Annals of Physics, 1915. 47: p. 879-885.
31. Lanczos, C. and B. Gellai, Fourier analysis of random sequences. Computers & Mathematics with Applications, 1975. 1(3-4): p. 269-76.
32. Wittig, L.E. and A.K. Sinha. Simulation of multicorrelated random processes using the FFT algorithm. Proceedings of the 85th Meeting of the Acoustical Society of America (abstracts only). 1973. Boston, MA, USA.
33. Wittig, L.E. and A.K. Sinha, Simulation of multicorrelated random processes using the FFT algorithm. Journal of the Acoustical Society of America, 1975. 58(3): p. 630-4.
34. Smith, J.I., A computer generated multipath fading simulation for mobile radio. IEEE Transactions on Vehicular Technology, 1975. UT-24(3): p. 39-40.
35. Nakamura, H., Y. Husimi, and A. Wada, An application of Fourier synthesis to pseudorandom noise dielectric spectrometer. Japanese Journal of Applied Physics, 1977. 16(12): p. 2301-2.
36. Lemke, M. and V. Richter, Synthesis of time-dependent signals for simulation experiments. VDI Zeitschrift, 1978. 120(10): p. 475-82.
37. Holmes, J.D., Computer simulation of multiple, correlated wind records using the inverse fast Fourier transform. Institution of Engineers, Australia, Civil Engineering Transactions, 1978. CE20(1): p. 67-74.
38. Aoshima, N. and Y. Miyagawa, Generation of Gaussian signals whose spectra are given arbitrarily by inverse Fourier transforms. Transactions of the Society of Instrument and Control Engineers, 1979. 15(3): p. 389-94.
39. Eckel, G., X. Rodet, and Y. Potard. A SUN-Mercury Workstation. Proceedings of the International Computer Music Conference. 1987. Champaign, Urbana, USA: CMA.
40. Depalle, P. and X. Rodet, Synthèse additive par FTT inverse. 1990,IRCAM, Paris France,.
41. Freed, A., X. Rodet, and P. Depalle. Synthesis and control of hundreds of sinusoidal partials on a desktop computer without custom hardware. Proceedings of the Fourth International Conference on Signal Processing Applications and Technology ICSPAT '93. 1993. Santa Clara, CA, USA: DSP Associates.
42. McAulay, R.J. and T.E. Quatieri, Processing of Acoustic Waveforms, Patent #4937873,1988, MIT.
43. Freed, A., Inverse Transform Narrow Band/Broad Band Sound Synthesis, Patent #5686683,1997, Regents of the University of California.
44. Marques, J.S. and L.B. Almeida. Sinusoidal modeling of speech: representation of unvoiced sounds with narrow-band basis functions. Proceedings of the EUSIPCO-88. 1988. Grenoble, France: North-Holland.
45. Carl, H. and B. Kopatzik. Speech coding using nonstationary sinusoidal modelling and narrow-band basis functions. Proceedings of the 1991 International Conference on Acoustics, Speech and Signal Processing (Cat. No.91CH2977-7). 1991. Toronto, Ont., Canada: IEEE.
46. Goodwin, M. Residual modeling in music analysis-synthesis. Proceedings of the ICASSP. 1996. Atlanta, GA, USA: IEEE.
47. Freed, A. and M. Wright, CAST: CNMAT's Additive Synthesis Tools. 1998,CNMAT,http://www.cnmat.berkeley.edu/CAST.
48. Wessel, D.L., Timbre space as a musical control structure. Computer Music Journal, 1979. 3(2): p. 45-52.
49. Tellman, E., L. Haken, and B. Holloway, Timbre morphing of sounds with unequal numbers of features. Journal of the Audio Engineering Society, 1995. 43(9): p. 678-89.
50. Risset, J.C. and D. Wessel, Exploration of Timbre by Analysis and Synthesis, in The Psychology of Music, D. Deutsch, Editor. 1982, Academic Press.
51. Marques, L.S. and L.B. Almeida, Frequency-varying sinusoidal modeling of speech. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989. 37(5): p. 763-5.
52. Marques, J.S. and L.B. Almeida. A background for sinusoid based representation of voiced speech. Proceedings of the IEEE-IECEJ-ASJ International Conference on Acoustics, Speech and Signal Processing (Cat. No.86CH2243-4). 1986. Tokyo, Japan: IEEE.
53. Tabei, M. and M. Ueda. FFT multi-frequency synthesizer. Proceedings of the International Conference on Acoustics, Speech, and Signal Processing. 1988. New York, NY.
54. Goodwin, M.M., Adaptive signal models : theory, algorithms, and audio applications, 1997, Ph. D. Thesis, Electronics Research Laboratory College of Engineering University of California.
55. Goodwin, M. and X. Rodet. Efficient Fourier synthesis of nonstationary sinusoids. Proceedings of the ICMC. 1994: ICMA.
56. Goodwin, M. and A. Kogon. Overlap-add synthesis of nonstationary sinusoids. Proceedings of the International Computer Music Conference. 1995. Banff, Canada: CMA.
57. Fitz, K. and L. Haken. Bandwidth Enhanced Sinusoidal Modeling in Lemur. Proceedings of the International Computer Music Conference. 1995. Banff, Canada.
58. Honghton, A.D., A.J. Fisher, and T.F. Malet, An ASIC for digital additive sine-wave synthesis. Computer Music Journal, 1995. 19(3): p. 26-31.
59. Phillips, D., A. Purvis, and S. Johnson, On an efficient VLSI architecture for the multirate additive synthesis of musical tones. 1997. 43(1-5): p. 337-40.
60. De Bernardinis, F., et al. A single-chip 1,200 sinusoid real-time generator for additive synthesis of musical signals. Proceedings of the EEE International Conference on Acoustics, Speech, and Signal Processing. 1997. Munich, Germany: IEEE Comput. Soc. Press.
61. Chaudhary, A., A. Freed, and L.A. Rowe. OpenSoundEdit: An Interactive Visualization and Editing Framework for Timbral Resources. Proceedings of the International Computer Music Conference. 1988. Ann, Arbor, Michigan.
62. Chaudhary, A., et al. A 3D Graphical User Interface for Resonance Modeling. Proceedings of the International Computer Music Conference. 1998. Ann Arbor, Michigan: CMA.
63. Wright, M. and A. Freed. OpenSynth Control: A New Protocol for Communicating with Sound Synthesizers. Proceedings of the International Computer Music Conference. 1997. Thessaloniki, Greece: ICMA.
64. Wright, A., et al. New Applications of the Sound Description Interchange Format. Proceedings of the International Computer Music Conference. 1988. Ann, Arbor, Michigan.
65. Freed, A. Bring Your Own Control Additive Synthesis. Proceedings of the International Computer Music Conference. 1995. Banff, Canada: ICMA.
66. Verge, M.P., et al., Sound production in recorderlike instruments .1. Dimensionless amplitude of the internal acoustic field. Journal of the Acoustical Society of America, 1997. 101(5 PT1): p. 2914-2924.
67. Verge, M.P., et al., Jet formation and jet velocity fluctuations in a flue organ pipe. Journal of the Acoustical Society of America, 1994. 95(2): p. 1119-32.
68. Verge, M.P., et al., Jet oscillations and jet drive in recorder-like instruments. Acta Acustica, 1994. 2(5): p. 403-19.
69. Warusfel, O., P. Derogis, and R. Caussé. Radiation Synthesis with Digitally Controlled Loudspeakers. Proceedings of the 103rd Convention of the AES. 1997. New York: AES, New York.
70. Meyer, D.G., Computer simulation of loudspeaker directivity. Journal of the Audio Engineering Society, 1984. 32(5): p. 294-315.
71. Weinreich, G., Directional tone color. Journal of the Acoustical Society of America, 1997. 101(4): p. 2338-46.
72. Derogis, P. and R. Causse, [Characterization of the Acoustic Radiation of the Soundboard of an Upright Piano]. Journal De Physique Iv, 1994. 4(C5): p. 609-612.
73. Wessel, D., Instruments That Learn, Refined Controllers, And Source Model Loudspeakers. Computer Music Journal, 1991. 15(4): p. 82-86.
74. Kendall, G.S., The decorrelation of audio signals and its impact on spatial imagery. Computer Music Journal, 1995. 19(4): p. 71-87.
75. Kendall, G.S., A 3-D sound primer: directional hearing and stereo reproduction. Computer Music Journal, 1995. 19(4): p. 23-46.