After a survey of inverse transform methods for the efficient
synthesis of narrow-band and broad-band signals, a novel spectral
line broadening technique is introduced for synthesis of pitch
modulated noise signals. This new transform-domain approach is
compared to the time-domain oscillator method with respect to
their relative efficiency on modern processors
The term "noise" is used to describe the perception of a multitude of features of sounds from musical instruments, for example:
The Sum of Sinusoid+Residual models
of McAulay/Quatieri, Serra/Smith, Depalle/Rodet, et al., have
proved useful for modeling and coding short musical tones. The
assumption of these models is that the residual is colored independently
of sinusoidal parameter estimates. This assumption is invalid
for most musical instruments so inadequate fusion of re-synthesized
noise and sinusoidal components is often observed. This is especially
troublesome when transformations are applied such as time scaling
and pitch shifting
The problem is that all forced oscillators (bowed strings,
voice, reeds, trumpets, flue pipes, etc.) generate nearly-periodically
modulated noise, not additive noise. A combination of a better
understanding of the physics of these oscillatory mechanisms (Rodet, 1993, Rodet,
1995) and new methods in higher order statistics (Brillinger
and Irizarry, 1998, Dubnov
and Rodet, 1997), wavelets (Goodwin
and Vetterli, 1996) and time series (Irizarry,
1998) are leading to better tools for multi-level decomposition
of sounds into transient events, pitched and unpitched oscillations,
convolutional noise and colored noise. These new models require
efficient, real-time noise synthesis algorithms. This paper contributes
an efficient implementation of one such algorithm for noise synthesis:
spectral line broadening.
Modulating the phase of a sinusoidal carrier with a random signal results in a narrow band noise source. This spectral broadening process has been used for decades in spread-spectrum radio frequency (RF) communications systems where it is usually implemented directly in the time domain. Musical applications of line broadening were explored by Risset and Wessel in the 1970s (Risset and Wessel, 1982).
With appropriate parameters for the noise amplitudes, sounds synthesized using spectral line broadening processes are perceived as similar to the noise found in voice and musical instruments such as flutes and flue pipes. Since the two noise generating mechanisms are quite different, it is interesting to consider what features the mechanisms have in common that may explain a similar percept. In the voice and aformentioned wind instruments, the noise process is the result of turbulence, the amplitude of which is dependent on air velocity, which is modulated by the nearly periodic primary oscillator. The fundamental frequency and partial amplitudes are not greatly influenced by the turbulence. This independence is a feature of the spectral line broadening process because of the use of a zero mean random phase modulation.
In physical systems the amplitude of the primary oscillator and turbulent noise are both proportional to driving energy. The amplitude parameter of the line broadening spectral synthesis process conveniently adjusts the amplitude of both elements. This parameterization is a convenient starting point for more sophisticated musical instrument models that dose noise and partial energy according to frequency and driving force.
A final important connection between sounds created by spectral
line broadening and modulated noise is that both are perceived
as originating from a single source. In contrast to additive noise
models, the integrity of spectral line broadened sources survives
musically useful transformations such as transposition, time dilation
and compression.
Implementing spectral line broadening efficiently with oscillator methods on modern, general-purpose microprocessors is surprisingly challenging. The first problem is that most pseudo-random sequence generators employ integer arithmetic operations, which are slower than floating point multiply/add operations on most processors. The second problem is that the noise signals have to be scaled to dose the line broadening before being added to the current phase (or frequency) of the oscillator. The scaling is fastest in floating point arithmetic, but on common processors, such as the PowerPC, conversion of the final phase back to an integer (for the sinusoidal table lookup) is prohibitively expensive.
No provision for spectral line broadening has been made to date in custom VLSI real-time systems for additive synthesis of music (De Bernardinis, et al., 1997, Honghton, et al., 1995, Phillips, et al., 1997). One reason for this is that the interface between the musical control software and the synthesis circuits is the primary performance bottleneck and increasing the number of parameters to send across this interface worsens the problem.
Transform-domain synthesis methods are an effective alternative
to time-domain oscillators. Because they exhibit good temporal
and spatial locality, implementations of transform-domain algorithms
can exploit the register, cache and main memory hierarchy of modern
computers. Communication bottleneck can be minimized by computing
the control and synthesis functions in a single address space
and by computing control functions at a frame rate, typically
around 1/100th of the output sample rate. After the
following survey of additive synthesis techniques, we present
a new algorithm for spectral line broadening using transform domain
techniques.
In the late 1970s, the availability of single chip digital multipliers stimulated the construction of digital signal processors for musical applications (Allen, 1985). Although these machines were capable of accurately synthesizing hundreds of sinusoids (DiGiugno, 1976), their prohibitive cost and limited programming tools prevented widespread use. A new signal synthesis method was needed that could better exploit the rapid advances in integrated circuit integration and computer architecture.
Since sinusoidal summation models involve spectral descriptions, the key to an efficient new algorithm for additive synthesis is an efficient transformation from frequency to signal domain. Although the Fast Fourier Transform (FFT) was widely known and used since its rediscovery and introduction in 1965 (Cooley and Tukey, 1965), the challenges to its use for continuous synthesis of multiple sinusoids were not surmounted until the 1970s. In a little known 1974 thesis, R.H. Davis (Davis, 1974) pioneered the two essential features of a synthesis window and overlap-add process.
The first musical application of the weighted overlap-add inverse FFT method is described in a book by Chamberlin (Chamberlin, 1980). The benefits of the method are not obvious from this exposition because of the poor performance of the triangular and sine-squared windows suggested and a lack of affordable computers for the FFT calculations.
The next important development came from the speech research community with the introduction of sinusoidal models for speech coding (McAulay and Quatieri, 1985). The inverse FFT method was applied to synthesize sinusoidally coded speech in 1988 (McAulay and Quatieri, 1988). In 1992 George and Smith described a musical tone synthesis scheme using the inverse FFT (George and Smith, 1992).
By the early 1980s the theory of transform domain synthesis of sinusoids and noise was well developed and had been applied in speech, music and other applications. More widespread application of this theory would require algorithms that efficiently exploited available computing machinery. In 1987 Rodet et al. developed tools for musical signal processing on an array coprocessor attached to a Sun workstation (Eckel, et al., 1987). Depalle and Rodet (Depalle and Rodet, 1990) developed an additive synthesizer based on the Inverse FFT for their musical workstation. This was the first real-time transform domain music synthesizer. By the early 1990s workstations and desktop computers were fast enough for real-time implementations of additive synthesis with hundreds of partials (Freed, et al., 1993).
Implementations of spectral line broadening in the transform
domain require a frequency domain description of a modulated sinusoid.
The analysis side of this problem was addressed by Marques and
Almeida (Marques and Almeida, 1986,
Marques and Almeida, 1989).
Tabei and Ueda (Tabei and Ueda, 1988)
explore the synthesis issues and Goodwin (Goodwin,
1997) sought efficient algorithms for non-stationary sinusoids
(Goodwin and Kogon, 1995, Goodwin and Rodet, 1994). Unfortunately
the key optimizations that make sinusoidal synthesis so efficient
in the transform domain depend on the narrow band property of
a constant frequency sine wave. This author has developed a novel
compromise (Freed, 1997) for synchronous
noise synthesis by adding random values to the phases of transform
values for each bin in the transform associated with each sinusoid.
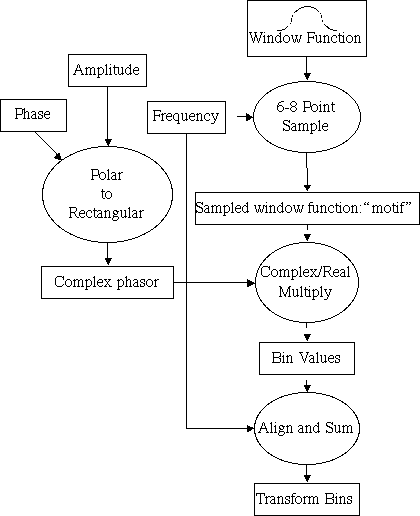
The computational kernel of transform domain sinusoidal synthesis is illustrated below:

A short, efficient inner loop instruction sequence iterates over each sinusoid in the set of partials. The inner loop length is minimized by exploiting a transform (e.g., Fourier) that localizes the energy of constant frequency, constant amplitude sinusoids. By careful choice of synthesis window and transform the number of spectral bins computed for each sinusoid can be reduced to around six with minimal audible artifacts. The inner loop samples the spectral transform of the synthesis window to yield a scale factor for each bin value. The bin values are computed by projection of the vector of the desired phase and amplitude. This polar-to-rectangular conversion is performed outside the inner loop, typically using tables for the sine and cosine calculation. The inner loop is thus reduced to a short sequence of real/complex multiplications and complex additions. The dozen or so instructions for the inner loop result in an entire frame of roughly a hundred samples of sound output.
Spectral line broadening may be introduced into the sinusoidal synthesis kernel by modulating the phase of the sinusoid by a scaled, zero-mean, uniform random value.
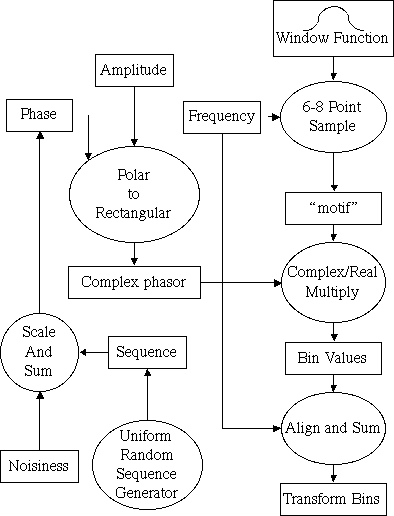
This additional computation is performed outside the inner loop and since the random sequence can be tabulated, the additional cost for spectral line broadening is smallc significantly smaller than the analogous computation for time-domain oscillator methods.
This algorithm has been added to CNMATs Additive Synthesis
Tools (CAST) (Freed and Wright, 1998)
and used to develop new synthesis models for flue pipe tones.
Spectral line broadening will be added to the transform-domai
synthesis module of a new real-time programming environment, OSW,
(Chaudhary, et al., 1999). We will
also explore its use with a new additive synthesis method based
on second-order recursive filters (Hodes
and Freed, 1999).
J. Allen (1985), "Computer
architecture for digital signal processing," Proceedings
of the IEEE, vol. 73, num. 5, pp. 852-73.
D. R. Brillinger and R. A. Irizarry
(1998), "An investigation of the second- and higher-order
spectra of music," Signal Processing, vol. 65, num.
2, pp. 161-179.
H. Chamberlin (1980), Musical
applications of microprocessors. Rochelle Park, N.J.: Hayden
Book Co.
A.
Chaudhary, A. Freed, and M. Wright (1999), "An Open Architecture
for Real-Time Audio Processing Software," presented at Audio
Engineering Society 107th Convention.
J. W. Cooley and J. W. Tukey (1965),
"An algorithm for the machine computation of complex Fourier
Series," Mathematics of Computation, vol. 19, pp.
297-301.
R. H. Davis (1974), "Synthesis
of steady-state signal components by an all-digital system,"
Ph. D. Thesis, Maryland.
F. De Bernardinis, R. Roncella, R.
Saletti, P. Terreni, and G. Bertini (1997), "A single-chip
1,200 sinusoid real-time generator for additive synthesis of musical
signals," presented at EEE International Conference on Acoustics,
Speech, and Signal Processing, Munich, Germany.
P. Depalle and X. Rodet (1990), "SynthHHse
additive par FTT inverse," IRCAM, Paris France.
G. DiGiugno (1976), "A 256 Digital
Oscillator Bank," presented at Computer Music Conference,
Cambridge, Massachusetts: M.I.T.
S. Dubnov and X. Rodet (1997), "Statistical
Modeling of Sound Aperiodicities," presented at International
Computer Music Conference, Thessaloniki, Greece.
G. Eckel, X. Rodet, and Y. Potard
(1987), "A SUN-Mercury Workstation," presented at International
Computer Music Conference, Champaign, Urbana, USA.
A.
Freed (1997), "Inverse Transform Narrow Band/Broad Band Sound
Synthesis," Patent #5686683, Regents of the University of
California.
A.
Freed, X. Rodet, and P. Depalle (1993), "Synthesis and control
of hundreds of sinusoidal partials on a desktop computer without
custom hardware," presented at Fourth International Conference
on Signal Processing Applications and Technology ICSPAT '93, Santa
Clara, CA, USA.
A. Freed and M. Wright (1998), "CAST:
CNMAT's Additive Synthesis Tools," CNMAT. http://www.cnmat.berkeley.edu/CAST
E. B. George and M. J. T. Smith (1992),
"Analysis-by-synthesis/overlap-add sinusoidal modeling applied
to the analysis and synthesis of musical tones," Journal
of the Audio Engineering Society, vol. 40, num. 6, pp. 497-516.
M.
Goodwin and A. Kogon (1995), "Overlap-add synthesis of nonstationary
sinusoids," presented at International Computer Music Conference,
Banff, Canada.
M.
Goodwin and X. Rodet (1994), "Efficient Fourier synthesis
of nonstationary sinusoids," presented at International Computer
Music Conference.
M. Goodwin and M. Vetterli (1996),
"Time-frequency signal models for music analysis, transformation,
and synthesis," presented at IEEE-SP International Symposium
on Time-Frequency and Time-Scale Analysis, Paris, France.
M. M. Goodwin (1997), "Adaptive
signal models: theory, algorithms, and audio applications,"
Ph. D. dissertation, Memorandum no. UCB/ERL M97/91, Electronics
Research Laboratory, Co llege of Engineering, University of California,
Berkeley.
T.
Hodes and A. Freed (1999), "Second-order recursive oscillators
for musical additive synthesis," presented at International
Computer Music Conference, Beijing, China.
A. D. Honghton, A. J. Fisher, and
T. F. Malet (1995), "An ASIC for digital additive sine-wave
synthesis," Computer Music Journal, vol. 19, num.
3, pp. 26-31.
R.
Irizarry (1998), "Statistics and Music: Fitting a Local Harmonic
Model to Musical Sound Signals," Ph. D. Thesis, UC Berkeley.
J. Laroche (1993), "Autocorrelation
method for high-quality time/pitch-scaling," presented at
IEEE Workshop on Applications of Signal Processing to Audio and
Acoustics, New York.
J. Laroche and M. Dolson (1997),
"Phase-vocoder: about this phasiness business,"; presented
at ASSP Workshop on Applications of Signal Processing to Audio
and Acoustics, New Paltz, NY.
J. Laroche, Y. Stylianou, and E.
Moulines (1993), "HNS: Speech modification based on a harmonic+noise
model,"; presented at IEEE International Conference on Acoustics,
Speech, and Signal Processing (Cat. No.92CH3252-4), Minneapolis,
MN, USA.
J. S. Marques and L. B. Almeida (1986),
"A background for sinusoid based representation of voiced
speech,"; presented at IEEE-IECEJ-ASJ International Conference
on Acoustics, Speech and Signal Processing (Cat. No.86CH2243-4),
Tokyo, Japan.
L. S. Marques and L. B. Almeida (1989),
"Frequency-varying sinusoidal modeling of speech,";
IEEE Transactions on Acoustics, Speech and Signal Processing,
vol. 37, num. 5, pp. 763-5.
R. J. McAulay and T. F. Quatieri
(1985), "Mid-rate coding based on a sinusoidal representation
of speech,"; presented at IEEE International Conference on
Acoustics, Speech, and Signal Processing, Tampa, FL, USA.
R. J. McAulay and T. F. Quatieri
(1988), "Computationally efficient sine-wave synthesis and
its application to sinusoidal transform coding,"; presented
at ICASSP, New York, NY.
D. Phillips, A. Purvis, and S. Johnson
(1997), "On an efficient VLSI architecture for the multirate
additive synthesis of musical tones," , vol. 43, num. 1-5,
pp. 337-40.
J. C. Risset and D. Wessel (1982),
"Exploration of Timbre by Analysis and Synthesis," in
The Psychology of Music, D. Deutsch, Ed.: Academic Press.
X.
Rodet (1993), "Models of musical instruments from Chua's
circuit with time delay," IEEE Transactions on Circuits
and Systems II: Analog and Digital Signal Processing, vol.
40, num. 10, pp. 696-701.
X. Rodet (1995), "One and two
mass Models of Oscillations for Voice and Instruments," presented
at Inernational Computer Music Conference, Banff, Canada.
M. Tabei and M. Ueda (1988), "FFT
multi-frequency synthesizer," presented at International
Conference on Acoustics, Speech, and Signal Processing, New York,
NY.