This paper summarizes our work adapting a recursive digital resonator for use on sixteen-bit fixed-point hardware. The modified oscillator is a two-pole filter with error properties expressly matched to use in the range of frequencies relevant to additive synthesis of digital audio. We present the algorithm, error analysis, performance analysis, and measurements of an implementation on a fixed-point vector microprocessor system.
The most widely used digital sinusoidal oscillator structure employs a first order recursion to accumulate and wrap a phasor, followed by a sinusoidal functional evaluation -- usually by indexing precomputed tables. Second order recursions are an attractive alternative because the sinusoid is computed within the structure, avoiding the need for a large table or specialized hardware function evaluator. Unfortunately, numerous theoretical and practical challenges have to be overcome to use second order structures. We are motivated to overcome these challenges because upcoming generations of microprocessors are hostile to efficient implementations of first-order recursive oscillators. Even when primary cache memory is large enough to hold a sine table, no locality of reference is observed for arbitrary frequencies. Getting good performance from vector microprocessors such as the Analog Devices TigerSharc and the Motorola Altivec and from VLIW (Very Long Instruction Word) machines such as the Intel IA-64 requires playing to the strengths of these SIMD (Single Instruction, Multiple Data) and VLIW machines: large multiply/add rate for on-chip data. The techniques described in this paper [1] were originally developed for a fixed-point vector microprocessor T0 [2]. Although these techniques were developed because T0 has no floating point unit, the highest multiply/add rate for many of the aforementioned machines is achieved when they operate on vectors of short fixed-point operands rather than vectors of floating point numbers; thus, our approach is directly applicable.
The primary challenge with digital recursive structures is managing long-term stability, since rounding and truncation errors accumulate. In most applications, frequency precision is more important than phase stability, and therefore the slow, long-term phase drift of first order oscillators is usually ignored. Error accumulation has more serious consequences in second order structures and, unfortunately, the most computationally efficient second order structure, the direct form I, is the most susceptible to debilitating instability at musically useful frequencies. An additional challenge of moderate-precision fixed-point arithmetic machines is providing sufficient frequency coefficient resolution.
Our novel approach to these challenges is two-fold: we keep individual oscillators short-lived, periodically recomputing state variables for each; and we modify the actual recursion calculation to increase frequency accuracy. Our algorithm shares some features of transform domain additive synthesizers [3]. The first similarity is that the output is computed by overlapping short vectors of signals. Each vector contains the sum of many fixed frequency, fixed amplitude sinewaves. Keeping these vectors short and choosing an appropriate window guarantees a seamless interpolation from frame to frame. The second similarity is that the frequency and amplitude of each sinewave are transformed into a new domain which offers efficiency advantages for the processor at hand. In the case of traditional transform domain additive synthesizers, a spectrum is built which can be transformed efficiently into a signal block using an inverse orthogonal transform, e.g., FFT. We choose to transform into the domain of second order recursive oscillator coefficients. Advantages over FFT methods include fewer constraints over the frame size (i.e., lower latency), no cross modulation distortion components, lower memory requirements, and lower algorithmic complexity. The major disadvantage is a higher cost per partial.
The general form of the digital resonator, with no damping or initialization impulse function, is:
with 
as the sampling
frequency, 
as the desired
(constant) frequency of oscillation.
To implement this equation using only sixteen-bit fixed-point multiplies, we needed to (1) manage the fixed-point units with enough precision to maintain accuracy across the entire audible frequency range, while (2) taking special care to provide sufficient frequency coefficient resolution to account for human ability to distinguish subtle differences in low frequencies. Accuracy must be maintained across a broader range and with more precision for low-frequency partials than a simple sixteen-bit fixed-point representation supplies. Additionally, because the frequency coefficient multiplication is in the critical path, we want to minimize the computational overhead of the changes.
To quantify the issue, we specify the minimum perceptible musical interval and then calculate the resolution necessary to maintain relative frequency accuracy. Doing so indicates that the low-frequency components require more precision than higher ones -- which is intuitive, since we are calculating relative accuracy. Thus, to minimize perceived error, we remap the frequency coefficient representations in two ways: we employ an exponent internally to emulate floating-point range extension, and invert the bit representation to bias accuracy toward low frequencies rather than high frequencies. These changes require two new operations per filter per sample: an add with constant shift and a variable shift.
To understand the modifications to the filter, recall the original
recurrence relation for our sine wave generator (with 
). At low frequency, the coefficient 
is very close to two, and so in a floating-point
format, lower frequencies synthesized using the formula will have
less accuracy than higher-frequencies due to the need to explicitly
represent the leading ones in the mantissa. Numbers closer to
zero benefit from the implicit encoding of leading zeros via a
smaller exponent. In other words, larger values require bits with
larger ``significance'' (absolute value), forcing the least significant
bits in the same word to also have higher significance, thus forcing
higher worst-case quantization error. We can more effectively
use the bits of the mantissa by reversing this relationship, recasting
the equation as:
i.e., where 
.
To represent 
, an unsigned
sixteen-bit mantissa m is combined with an unsigned exponent
e, biased so that the actual represented value is 
. Thus, the exponent is also the right shift
amount necessary to correct a 16b 
16b 
32b multiply
with as an operand.
The two in the exponent allows
to range from 0 to 4 when m is interpreted as a fractional
amount and f ranges between zero and the Nyquist frequency.
What is achieved with this remapping of number representation
is the ability to represent lower frequencies with more significant
bits by mapping higher frequencies to representations with less
significant digits. In particular, as 
varies from -2 to 2, we define
to vary from 4 to 0. Smaller frequency values produce smaller
values of , helping to
satisfy our asymmetric accuracy requirements.
Relative frequency discrimination is based on the ratio of
adjacent frequencies. To determine worst-case relative error,
we wish to determine the maximum ratio between two adjacent values. Call these frequency coefficients
and 
, and their corresponding frequencies 
and 
. From the
definition of 
and the equation
,
Taking any two adjacent numbers in the range, we can compute
with Eq. 2.
Evaluating this ratio for all possible adjacent pairs of epsilon
values allows us to determine that it is maximized for 
and 
, where 
. This ratio
is lower than the minimum frequency ratio humans are able to differentiate,
a pitch difference of approximately four to five cents (about
1/25-1/20 of a semitone) [4].
The maximum error of our algorithm is actually less than two cents:
.
This calculation illustrates that by designing higher values to coincide with higher represented
frequencies, we achieve a good match of the numerical representation
to the asymmetric accuracy requirements of human logarithmic pitch
perception.
Two tones that are meant to have an exact ratio in their frequencies may instead generate beat frequencies due to frequency quantization. This effect, caused by absolute error, should be minimized.
Worst-case absolute error due to epsilon quantization is shown in Figure 1, which contains both a side-by-side comparison below 2000 Hz and a detail for the modified form. As expected, the recast filter maintains more precise absolute frequency than the original form.
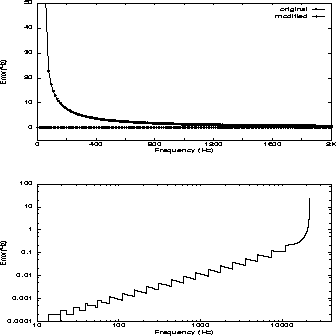
Fundamentally, more than 16 bits of fractional coefficient are necessary to obtain 1 Hz absolute precision across the audible spectrum [5]. Our method maintains reasonable error bounds in sixteen bits of mantissa by scaling these bits with the exponent.
At each iteration of the recursive form, a small error is introduced due to rounding of the multiply result. Due to the recursion, this error isn't corrected until reinitialization of the state variables. Possible effects of this include degradation of the signal-to-noise ratio, degradation of the long-term phase accuracy, and a lack of amplitude stability -- all of which can cause audible artifacts.
As has been illustrated elsewhere [6], this can be corrected via additional computation. To avoid this, we exploit our ability to reinitialize the computation at overlap-add frame boundaries, thereby allowing use of a non-self-correcting (but higher-performance) oscillator form.
The resonator can be initialized to a desired frequency and
phase at sample 
by properly
choosing the two state variables 
and 
using function
evaluations in place of an initialization forcing function. The
lookup values for a sinusoid with phase p and frequency
f are:
These initializations must be accurate down to the low-order
bits in a 32-bit fixed point representation, with the binary point
set between the third and fourth bit positions in order to support
a phase in the range 
. Additionally, we need to compute the frequency coefficient 
to 32-bit accuracy.
These initial evaluations can be computed more quickly by rewriting
the equations for
and in a form that
requires only the computation of 
, 
, 
, and 
:
and 
with a hybrid technique: table-lookup for 
and Taylor expansion for 
combine to give an accurate 32-bit result
efficiently.
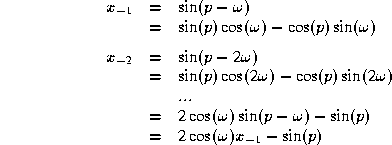
It may seem that this has actually increased the amount of
work we need to perform because there are now four trigonometric
evaluations rather than three (two initialization sines plus the
cosine in the recursive form). However, this approach turns out
to be more efficient by allowing for the judicious sharing of
intermediate values in a tandem sine and cosine generation procedure.
The tandem subroutine returns both
and for 
to full 32-bit fixed-point precision using
a hybrid technique combining table-lookup and Taylor expansion.
This keeps both the table size manageable (2048 entries of 32
bits) and the number of terms in the Taylor expansions small (two).
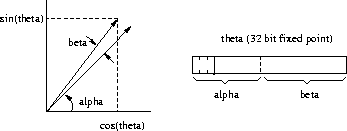
It is implemented by separating 
into and as shown in Figure 2;
is the high-order 11 bits of , and
the remaining low-order bits.
is used in an exact (to one LSB) 11-bit 32-bit table-lookups, while (guaranteed small)
is used in Taylor expansions:
The accuracy of expanding each to only two terms is guaranteed
by limiting the size of
to only the low-order 21 bits of
: the sum of the remaining terms in each expansion sequence, for
all , is less than
the LSB. Finally, and are combined using the relationships:
We implemented our approach on the SPERT neural network and signal processing accelerator board [7]. The SPERT houses a T0 chip [2], which tightly couples a general-purpose scalar MIPS core to a high-performance vector coprocessor. T0 is representative of digital signal processing architectures in its use of fixed-point arithmetic. Computing summations of oscillators for additive synthesis with an overlap-add approach using Eq. 1 and our pseudo-floating-point format, we need four multiplies, two variable shifts, two fused (constant) shifts and adds, and two regular adds:
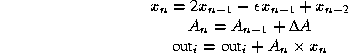
On T0, this requires a total of 
vector arithmetic operations per sinusoid when unrolled n
times. Unrolling four times due to trade-offs in register file
pressure on T0, we achieve best-case performance of about 1.15
cycles/partial: two fixed-frequency sinusoids are required per
variable-frequency partial because of overlap-add, 9 
operations are required per sine, two cycles
are required per vector operation on T0, and the vector length
is 32 elements. Thus, for our prototype SPERT board performing
8 operations per cycle (peak) with a 40 MHz clock rate and at
a 44.1 kHz sampling rate, a theoretical maximum of 768 partials
can be achieved in real time excluding all overhead. The current
implementation supports up to 608 simultaneous real-time partials
with frame lengths of 5.8 ms or greater, or about 1.5 cycles per
partial per sample.
Work on variable representations for direct-form oscillators and their associated error properties has been reported in the literature [8, 9], but none specifically matched for use with audio synthesis or SIMD/VLIW architectures. Low-frequency recursive oscillation was implemented on the TI TMS32010 DSP [10] using three 16-bit multiply stages and self-modifying code to hard-code shift values. As we have shown, the additional multiplies are unnecessary for audio applications.
We have summarized our work adapting a recursive digital resonator for use on sixteen bit fixed-point hardware, where the error properties are expressly matched for use in the range of frequencies relevant to additive synthesis of digital audio. The new technique allows for reliable computation of frequencies impossible to handle with the direct form, while keeping additional frequency precision costs down to only two additional operations per filter sample. We presented the algorithm, an error analysis, a performance analysis, and measurements of an implementation on a fixed-point vector microprocessor system. More detailed information is available elsewhere [1].
The authors would like to thank John Wawrzynek, John Hauser, David Wessel, Matt Wright, and Tristan Jehan for their assistance with this work and/or comments on this paper.
Todd Hodes
