A Compact 120 Independent Element Spherical
Loudspeaker Array with Programmable Radiation Patterns
Rimas Avizienis1, Adrian Freed2, and Peter Kassakian3 and David Wesel,4
April 2006
1 rimas@cnmat.berkeley.edu
2 adrian@cnmat.berkeley.edu
3kassak@cnmat.berkeley.edu
4wessel@cnmat.berkeley.edu
ABSTRACT
We describe the geometric and engineering design challenges that were overcome to create a new compact, 10-inch diameter spherical loudspeaker array with integrated class-D amplifiers and a 120 independent channel digital audio interface using Gigabit Ethernet.
A special hybrid geometry is used that combines the maximal symmetry of a triangular-faceted icosahedron with the compact planar packing of 6 circles on an equilateral triangle ("billiard ball packing"). Six custom 1.25inch drivers developed by Meyer Sound Labs are mounted on each of 20 aluminum triangular circuit boards. Class D amplifiers for the six speakers are mounted on the other side of each board. Two pentagonal circuit boards in the icosahedron employ Xilinx Spartan 3E FPGA's to demultiplex digital audio signals from incoming Gigabit Ethernet packets and process them before feeding the class-D modulators. Processing includes scaling, delaying, filtering and limiting.
1. Introduction
The array we describe has the largest driver count of a
series we have constructed based on the platonic solids [1, 6]. These arrays can be used to
synthesize radiation patterns of musical instruments, to create a monopole
source for room measurements and to create directional beams and nulls. The
mathematical basis of the signal processing applications for these arrays has
been published already [4, 5]. In this paper we focus on
the geometric considerations and engineering design constraints that led to our
latest array. We also briefly
discuss the systems-level control software for the array. Details of the
directivity control software itself and measurements of the array will be part
of a future publication when we complete careful acoustic characterization and
optimizations.
2.
Geometric Constraints
The key parameter to achieving good directivity control at high frequencies is to maximize the number of closely spaced drivers. The quality of control depends also on how evenly spaced the drivers are. The 2D version of this problem is easy: centering circular loudspeakers at the vertices of equilateral triangles tiling the plane yields the most efficient arrangement in a space filling sense. For a spherical array we have to embrace the challenges of the regular polygonal tilings in 3D and exploit the many useful properties of the platonic solids: equal spacing of neighboring face centers, faces tangential to the same insphere of the solid, and tangent points at the center of each face. The symmetries of these shapes often allow us to rotate a desired response without recomputing a filter design by simply changing amplitude scaling factors.
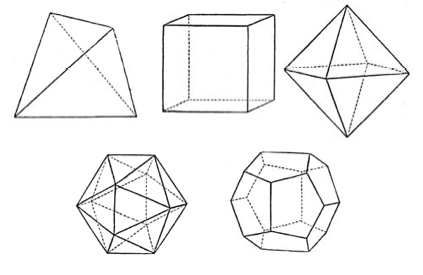
Figure 1. The Platonic Solids
2.1. Volumetrically efficient Platonic Solids
As well as having fewer faces the tetrahedron, cube and octahedron are much less efficient in terms of volume than the largest Platonic solids: the dodecahedron and icosahedron. Since most practical drivers for this application are circular the type of polygonal face is also relevant as the output power of the overall system will depends on how large a driver can be installed in each face. The platonic solid that yields the best volume efficiency and area efficiency is the dodecahedron. For this reason we built a "wide-band" dodecahedral array using long-throw 4-inch drivers with independent baffle chambers to improve low-frequency response [7].

Figure 2. Dodecahedral Speaker Array
Although we realized the basic wideband goal for monopole and dipole patterns, the driver spacing proved insufficient for high quality directivity control at high frequencies and for higher spherical harmonics [6]. The only solution to this is to increase the number of independent drivers. Since the icosahedron offers only a minor improvement over the dodecahedron we had to abandon the equally-spaced driver constraint and settle for a geometric arrangement with approximately even spacing.
2.2. Circular Packings on the Sphere
The first design we explored is the optimal packing of circles on the sphere using the tabulations of optimal spherical codes that are readily available [2]. Although this approach is very efficient in terms of area and volume, numerous practical problems would have to be solved. It is hard to build accurate spheres and accurately place drivers on them and the packing is so area efficient it is difficult to find enough room to attach a mounting or suspension structure. Finally, the lack of symmetries complicates the control software.
2.3. Geodesic Spheres
Another interesting geometry is the geodesic triangulation of a polyhedron such as the 80-faced, triangulated-in-4 icosahedron.

Figure 3. Geodesic sphere approximation
This does yield a solution with some symmetries and a hemispherical "seem" facilitating construction and maintenance. Unfortunately some of the face triangles are not equilateral and have varying dihedral angles negatively impacting area efficiency and directivity control quality.
2.4. Archimedian Solids
We can avoid the dihedral angle issue of the geodesics by using some of the larger members of the 13-strong Archimedian solid family, i.e., the 36-sided truncated icosahedron (soccer ball) and the 62-sided rhombicosidodecahedron.
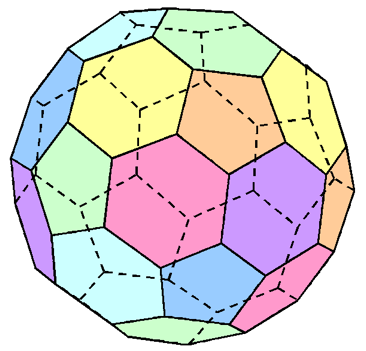
Figure 4 . A Truncated Icosahedron
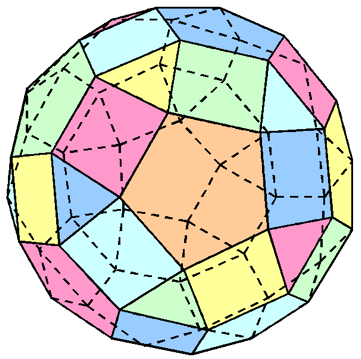
Figure 5. A Rhombicosidodecahedron
These solids have faces with more than one regular polygonal shape. This requires different driver sizes or some compromise in area and volume efficiency to use the largest single driver diameter that fits all the face shapes.
3. Engineering Constraints
3.1. Amplification
The final geometry we selected arose by considering the implications of a further practical constraints especially the lack of commercially available compact amplifiers to drive large speaker arrays. The amplifiers for our dodecahedral speaker are larger than the speaker itself and the wiring between them was an expensive, multi-core cable. By integrating the amplifiers within the array we avoid the long cable, increase reliability and lower cost of ownership of the system.
Flat circuit boards don't stack very efficiently within spherical structures and flexible circuit boards would have been challenging as we have to cool the electronics efficiently. We decided to attach flat circuit boards to aluminum plates that serve as a structural element to mount the speakers on, as heat sinks and EMI shield. Since efficient class-D controller chips are readily available for 6 or 8 channels we sought an appropriately shaped single "module" from which to assemble a polyhedron [3]. The best unit we found is simply an equilateral triangle. This allows us to use the optimal symmetric packing of circles in equilateral triangles, i.e., the "billiard ball" packings.
3.2. Class-D Chip Set Channel Efficiency
The “billiard ball” packings follow the sequence 1, 3, 6, 10, (n+n*n)/2. With 1.25inch diameter drivers the space-efficient match for the class-D chip set we used was 6; 20 of these equilateral triangle modules form the tetrahedron from which we built our 120 speaker array.

Figure 6. Controller side of 6-channel Class-D Amp.
Each amplifier board contains a Class-D controller (bottom of Figure 6), balanced output reconstruction filters (LCR) and 6 MOSFET driver chips (Figure 7). The controller does clock regeneration, digital to pulse conversion and thermal monitoring of the driver chips.

Figure 7. Driver and Heat-sink side of 6-channel Amp.
Two parallel pentagonal circuit boards (Figure 8) near the center of the icosahedron employ Xilinx Spartan 3E FPGA's to demultiplex digital audio signals from incoming ethernet packets and process them before feeding the class-D modulators.
Using two cards allows us to split the in two parts that resemble broken dinosaur egg shells and to rationalize the extensive wiring required between the control and amplifier boards for power, clock and data distribution. Each half of the array can be operated independently and they sit conveniently and stably on a bench for testing.

Figure 8. One of two Controller/interface Boards
A special daughter card for the controller board was developed to allow digital connections to an Audio Precision audio analyzer. This was essential for optimizing the circuit board layout of the amplifier boards. This layout and the output filter component choice turned out to be critical and very challenging parts of the project. PCB trace lengths and routing play an important role in achieving the potential of class-D amplifiers and the triangular board constraint made it impossible to adapt layouts already debugged by the chipset supplier and other builders using rectangular circuit boards. The close proximity of all the parts and high power high frequency traces made it essential to carefully shield the jitter attenuating clock recovery circuits in the controller.
3.3. Energy Storage Component Density
We considered a 60 driver array using a “diamond” module of two equilateral triangles with three drivers on each. It would have the interesting property that all drivers have the same spatial relationship to their neighbors throughout the array and according to simulations would perform quite well. It would however have to be significantly smaller than our 120 speaker array allowing too little room for the large passive components and digital interfacing circuitry required as illustrated in figure 9.

Figure 9. Volume-filling Toroidal Inductors and Decoupling Capacitors
3.4. Cooling, Cable Access and Mountability
The 120 driver array has less symmetry than a 60 driver array in the sense that drivers in our array fall into two equivalence classes, with vertex and edge relationships.
The optimal planar packing results in small gaps in coverage at the 10 vertices of the array. We could attempt to fill these gaps with additional drivers but chose instead to exploit them to provide air flow through the array and to provide access for cable and mounting/suspension options (see Figure 10).

Figure 10. Pentagonal access holes at the vertices
Meyer Sound Labs. contributed the custom built silk-dome drivers we use in the array. They are 1.25 inches in diameter and have a very narrow circular surround. This kind of driver would usually be used with a crossover filter as a tweeter in a conventional speaker. We operate these drivers at lower frequencies where they are not acoustically efficient so we have to protect them from thermal overloads and keep them within physical excursion limits. This is very important in arrays of this type because large power levels are required to create the cancellations necessary to achieve the desired radiation patterns. With the number of drivers involved, individual closed-loop temperature and excursion control would have been prohibitively expensive and complex so we have put the protection into the FPGA algorithmically using multiband limiters carefully designed to protect the array and also allow for short-term power peaks typical of musical material [4].
Although class-D amplifiers reach efficiencies of90% or more this is usually at high output power levels, (in our case 20-40W/channel). Our continuous power output level goal is 5W/driver where efficiencies are approximately 50%. The number of drivers in a relatively small space create significant thermal design constraints that we satisfy by a combination of the vertex holes to provide convective airflow and the use of aluminum and thermally conductive heat sink interfacing components.
3.5. Non-Ideal Polar Response of the Drivers
Mounting the drivers on triangular faces results in the vertex drivers being more distant from the center of the insphere of the array than the edge drivers. Also the line of rotational symmetry of the drivers does not pass through the center of the insphere.
We could have compensated for this using an offsetting "rack" for each driver, but for this and the other compromises mentioned above we have chosen to exploit the power of our convex optimization software and the affordable real-time signal processing integrated into the control electronics. We have to implement these features anyway to compensate for the actual polar radiation responses of the drivers. Our confidence in this approach is supported by Meyer Sound Labs reputation for manufacturing very consistent, high-quality drivers and the simulation results in Figures 11-14 that illustrate the potential directivity control quality using the error analysis methodology developed for our dodecahedron [6]. These plots show worse case errors for steered spherical harmonics of varying degrees at varying frequencies. The darker lines at lower heights on the plots indicate desirable values (the least error from ideal spherical harmonic synthesis).
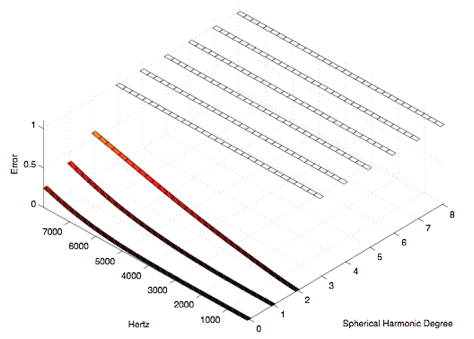
Figure 11. Twelve Driver Dodecahedron
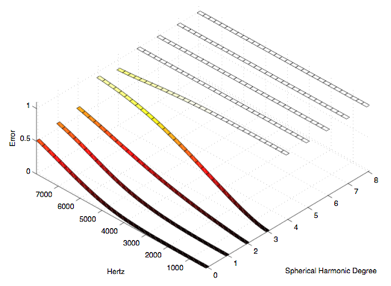
Figure 12. Twenty Driver Icosahedron
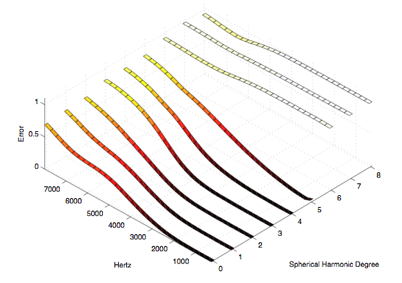
Figure 13. 60 Driver Icosahedron Simulation
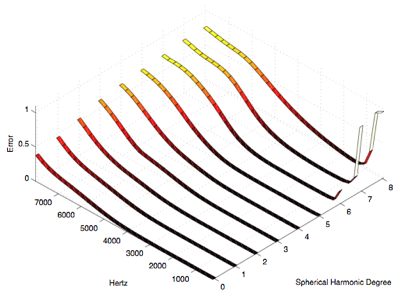
Figure 14. 120 Driver Icosahedron Simulation
4. Control Firmware and Software
4.1. Firmware
The FPGA firmware is developed in VHDL and also by direct synthesis from matlab. Processing includes configuration, monitoring, gain, delay, filtering and limiting. The firmware also implements input and output assembly, disassembly and buffering of ethernet packets that flow over a Gigabit Ethernet to host computers
4.2. Host Software
We chose Gigabit Ethernet because it is a relatively
simple industry standard and is efficiently implemented in modern computers:
most modern laptops and motherboards provide a contention free path to the main
processor for ethernet traffic. We have found it necessary to make small
modifications to the ethernet drivers in OS/X and linux to avoid priority
inversion problems and move data reliably and with low latency from audio
applications to the array. We have also demonstrated the capability of
combining packets from multiple host computers for applications where the load
of the steering algorithms is spread over a cluster of independent computers.
5. Conclusion
The spherical array described here is an essential tool for exploration of the effectiveness of programmable directivity algorithms. It will guide and inspire new and unusual applications in acoustic measurement and artistic endeavors. By carefully characterizing its performance we will be able to guide designs of future high-driver-count arrays.
6. acknowledgements
This work was supported by Meyer Sound Labs. and the UC Discovery Grant in Digital Media from the University of California’s Industry-University Cooperative Research Program (IUCRP).
7. REFERENCES
1. Baird, J., Meyer, J., Meyer, P., Kassakian, P. and Wessel, D., Controlling Loudspeaker Array Radiation in Three Dimensions. in 111th Audio Engineering Society Convention, (New York, NY, 2001).
2. Conway, J.H., Sloane, N.J.A. and Bannai, E. Sphere packings, lattices, and groups. Springer, New York, 1999.
3. Fuse, T. Unit origami : multidimensional transformations. Japan Publications : Distributed by Kodansha International/USA, Tokyo, Japan ; New York, 1990.
4. Kassakian, P. Convex Approximation with Applications in Magnitude Filter Design and Beamforming EECS, University of California Berkeley, Berkeley, 2006.
5. Kassakian, P., Magnitude Least-Squares Fitting via Semidefinite Programming with Applications to Beamforming and Multidimensional Filter Design. in IEEE International Conference on Acoustics, Speech, and Signal Processing, (Philadelphia, PA, USA, 2005), IEEE.
6. Kassakian, P. and Wessel, D., Characterization of Spherical Loudspeaker Arrays. in 117th Audio Engineering Society Convention, (San Francisco, 2004), AES.
7. Kassakian, P. and Wessel, D., Design of Low-Order Filters for Radiation Synthesis. in 115th Audio Engineering Society Convention, (New York, NY USA, 2003).