
The idea of synthesizing sounds by summing sinusoidal oscillations [Helmholtz 1863] has intrigued generations of musical instrument builders. Thaddeus Cahill's electromechanical implementations at the beginning of this century [Nicholl 93] illustrate graphically the basic challenge faced by these engineers--the creation of a large number of oscillators with accurate frequency control. Cahill used dynamos constructed from wheels of different sizes attached to rotating shafts ranging in length from 6 to 30 feet. The speed of each shaft was adjusted to obtain the required pitch. A total of 145 alternators were attached to the shafts. Since the vacuum tube and transistor (inventions of this century) were unavailable to Cahill, each rotating element had to produce nearly 12000 to 15000 watts of energy to deliver synthesized music to subscribers' homes.
In the late 1970's, the availability of single chip digital multipliers stimulated the construction of digital signal processors for musical applications [Allen 85]. Although these machines were capable of accurately synthesizing hundreds of sinusoids [DiGiugno 76], their prohibitive cost and limited programming tools precluded widespread use.
One hundred years after Cahill's work, despite rapid gains in computational accuracy and performance, the state of the art in affordable single chip real-time solutions to the problem of additive synthesis offers only 32 oscillators. Since hundreds of sinusoids are required for a single low pitch note of the piano, for example, current single chip solutions fall short by a factor of at least 20. A new technique for additive synthesis, FFT-1 [ Depalle&Rodet 90], offers a performance improvement of this order. This technique also provides an efficient method for adding colored noise to sinusoidal partials, which is needed to successfully synthesize speech and the Japanese Shakuhachi flute, for example. The FFT-1 algorithm itself has been described in detail elsewhere [Freed et al. 93]. This paper will focus on the implementation of additive synthesis on a workstation computer system, the SGI Indigo.
Although the FFT-1 algorithm is based on well-understood and simple principles [Nawab&Quatieri 88], an efficient implementation requires careful attention to detail. Programming errors and overzealous application of approximations for the sake of efficiency commonly result in artifacts in synthesized sounds that are hard to identify simply by listening. For this reason a reference implementation of additive synthesis was created using the digital oscillator method, commonly used in frequency synthesizers [Tierney et al. 71]; this reference implementation also serves as a yardstick with which the FFT-1 implementation may be measured. In order to put these two workstation implementations of additive synthesis in perspective, two other options will be considered-a DSP chip and a custom VLSI chip. In order of increasing cost of development, the implementation options are oscillators in C, FFT-1 in C, oscillators a DSP chip and oscillators in VLSI.
Assuming linear amplitude and frequency interpolation, the operations required for one sample for each oscillator can be broken down as follows:
| Operation | Adds | Multiplies | Modulo | Lookup |
| amplitude interpolation | 1 fp | |||
| frequency interpolation | 2 | |||
| sine evaluation | 1 | 1 | ||
| output accumulation | 1 fp | 1 fp |
Since there are no second order data dependencies in the lookup table oscillator all of the above operations can be performed in theory simultaneously by providing 4 adders, 1 multiplier, 1 shifter, and a table with a length which is a power of two. In current VLSI technology the table lookup operation has the longest latency. Oscillators based on higher order recursions [Smith&Cook 1992] and CORDIC operations [Hu 1992] have been proposed, but implementations have not yet demonstrated significant performance advantages over the direct table lookup oscillator. This is because the cost saving associated with avoiding a table lookup is offset by the additional cost of maintaining and accessing additional state variables, handling the interaction between frequency and amplitude controls [Gordon&Smith 85], and managing the effects of finite wordlength [Abu-El-Haija&Al-Ibrahim 86]. It is therefore reasonable to assume that a VLSI designer might choose the lookup table option for a fully custom chip. In the graph that follows the clock rate of the hypothetical VLSI custom chip was chosen to be 50MHz with 4 clock cycles required per oscillator per sample. The DSP chip was taken to be 50MHz and it was assumed that twenty clock cycles per sample per oscillator are required. These represent challenging but feasible goals with current technology. The SGI Indigo C code measurements correspond to a MIPS R4000 with a 100MHz internal clock.

The line for the FFT-1 does not pass through the origin because of the fixed cost of the inverse FFT operation, which has to be performed independently of the number of oscillators. Notice that on modern processers it represents less than one tenth of available performance.
The explanation for the excellent performance of the workstation software over custom hardware solutions lies in the clock rates. General purpose workstation processors are flagship products for semiconductor vendors and therefore win over DSP and custom ASIC's in the competition for the highest speed VLSI circuit manufacturing process. Because of the enormous investment required for new manufacturing processes (hundreds of millions of dollars) and the cost sensitive nature of DSP and custom ASIC applications, it is unlikely this situation will change in the near future. Note also that modern processors have incorporated most of the performance enhancing features of DSP chips [Lee 89].
The obvious conclusion to be drawn from this evaluation is that for computer music research no computing performance penalty need be paid as a result of choosing general purpose computer workstations over special purpose hardware options. However, computing performance is not the only issue in the choice of tools for computer music. A good computer music workstation must be able to provide appropriate real-time guarantees, accept sources of gestural input and control, and provide for audio input and output. Finally, it must be a productive platform for the broad range of computing paradigms researchers are exploring. The next sections consider each of these issues in turn.
The FFT-1 and Oscillator implementations for the SGI use the HTM system [Freed 92]. HTM includes a simple scheduler which uses commonly available UNIX operating system services to provide real-time performance with acceptable latencies of a few milliseconds. These services include the select system call to minimize unnecessary context switching overhead, plock to prevent memory from being swapped to disk, and schedctl to specify high priority, non-degrading process priorities. Although the form of these system calls is evolving as vendors reach agreement on real-time UNIX facilties, their function is available on most recent versions of UNIX.
The SGI Indigo, like most workstations and personal computers, provides serial ports that can be configured to support MIDI. These serial ports can also be used for other gestural input devices commonly used in Silicon Graphics' traditional user community, for example, 3 dimensional pointing devices and gloves. Another very flexible mechanism available for gestural input and control turns out to be the ethernet port. Ethernet is now cheaper per transferred bit than serial protocols such as MIDI. In small networks, typical of computer music research centers and private studios, real-time network performance may be easily obtained. For exploration of sophisticated control strategies for musical performance in a network environment, the MAX language [Puckette&Zicarelli 90] running on a Macintosh can be used with synthesis algorithms running on the SGI Indigo as illustrated below:
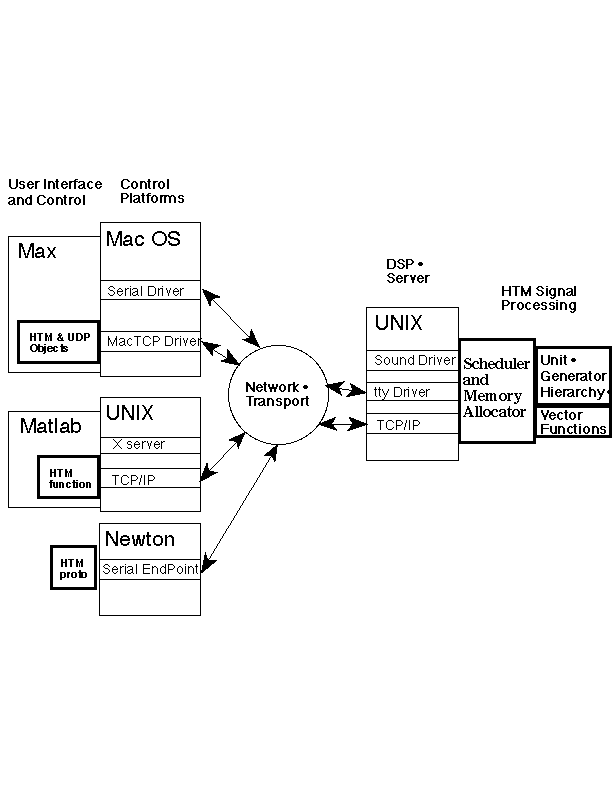
The emergence of multimedia applications has led to the incorporation of audio input and output hardware on the motherboards of workstations and personal computers. Currently, two channels each of analog input and output and digital input and output is standard practice. Some products announced this year include 4 channels of analog input and output.
HTM is able to minimize latency and jitter by taking advantage of an important feature that SGI offers in their audio hardware driver-the ability to know the number of sound samples in the input and output queues. The absence of such a feature or other mechanism in workstations will frustrate the implementation of responsive real-time sound synthesis.
The ability to choose between a wide range of sample rates (8kHz - 48kHz) was found to be very useful during development of synthesis software. For example, it allows a program slowed down by debugging code to still execute in real-time, at the sacrifice of output bandwidth.
Although effective development tools are emerging for DSP chips and custom VLSI processors, better programming tools are offered for workstation processors. The high quality of the code generated by modern C compilers is essential to achieve the numerical performance required in musical signal processing applications. For the FFT-1 implementation, several attempts were made to improve on code generated by the MIPS C compiler by coding in assembly language. These attempts were arduous and failed. The C compiler appears to optimally compile most critical numerical code for the R4000.
The ability to accurately measure performance of code execution down to the detailed level of the line of C source code has proven invaluable in tuning critical signal processing programs for musical applications. The operating system and hardware features to support this timing facility are rarely available in DSP and custom hardware systems.
Researchers are attacking the problem of synthesis control with a range of computing paradigms. These include signal estimation and modelling techniques [McAulay&Quatieri 86, Serra 86, Galas&Rodet 90-91], data flow, visual programming in MAX, numerical mathemetics using an HTM communications function in Matlab, statistical techniques [Garcia 92, Sandell&Martens 92], connectionist models [Lee&Wessel 92] and fuzzy control [Lee&Wessel 93]. Three dimensional visualization tools [Peevers 93] are also very useful, as illustrated below.

General purpose processors such as those found in workstations are the best choice to achieve balanced performance in these diverse computing paradigms required by musical applications.
Several years of experimentation with the FFT-1 algorithm for additive synthesis have indicated that the method provides excellent control over a wide range of sounds of high quality. Experience with implementations on affordable desktop workstations suggest that a low-cost real-time multi-timbral instrument based on FFT-l is within reach. It would have all the capabilities of present day synthesizers, plus many others such as the precise modifications of recorded sounds, as well as speech and singing voice synthesis.
The authors gratefully acknowledge the support of Gibson, Silicon Graphics and Zeta music. Alan Peevers provided the 3 dimensional analysis plot. Mike Goodwin offered many helpful suggestions during the preparation of this paper.
[Haija&Ibrahim 86] A. I. Abu-El-Haija & M. M. Al-Ibrahim, "Improving Performance of Digital Sinusoidal Oscillators By Means of Error Feedback Circuits,":, IEEE Trans. on Circuits and Systems, Vol. cas 33, no. 4, April 1986.
[Allen 85] J. Allen, "Computer architectures for digital signal processing," Proc. of the IEEE 73(5), 1985.
[Depalle&Rodet 90] P. Depalle & X. Rodet, "Synthèse additive par FTT inverse," Rapport Interne IRCAM, Paris 1990.
[DiGiugno 76] G. DiGiugno, "A 256 Digital Oscillator Bank," Presented at the 1976 Computer Music Conference, Cambridge, Massachusetts: M.I.T., 1976
[Freed 92] A. Freed, "Tools for Rapid Prototyping of Music Sound Synthesis Algorithms and Control Strategies", Proc. Int. Comp. Music. Conf., San Jose, CA, USA, Oct. 1992
[Freed 93] A. Freed & X. Rodet & P. Depalle, "Synthesis and Control of Hundreds of Sinusoidal Partials on a Desktop Computer without Custom Hardware," Proc ICSPAT, 1993.
[Galas&Rodet 90] T. Galas & X. Rodet, "An Improved Cepstral Method for Deconvolution of Source Filter Systems with Discrete Spectra", Int. Computer Music Conf., Glasgow, U.K., Sept. 90.
[Galas&Rodet 91] T. Galas & X. Rodet, "Generalized Discrete Cepstral Estimation of Sound Signals" IEEE Workshop on Application of Signal Processing to Audio and Acoustics, Oct. 1991.
[Garcia 92] G. Garcia, "Analyse des signaux sonores en termes de partiels et de bruit. Extraction automatique des trajets fréquentiels par des Modèles de Markov Cachés," Memoire de DEA en Automatique et Traitement du Signal, Orsay, 1992.
[Helmholtz 1863] H. L. F. von Helmholtz, "On the Sensations of Tone as a Physiological Basis for the Theory of Music", 1863, Translation of the 1877 Edition, Dover, 1954
[Gordon&Smith 85] J. W. Gordon & J. O. Smith, "A Sine Generation Algorithm for VLSI Applications," Proc. of ICMC 1985, Computer Music Association.
[Hu 92] Yu Hen Hu, "CORDIC-Based VLSI Architectures for Digital Signal Processing," IEEE Signal Processing Magazine, July 1992.
[Lee 88] E. A. Lee, "Programmable DSP Architectures", IEEE ASSP Magazine, October 1988.
[Lee&Wessel 92], M. Lee & D. Wessel, "Connectionist Models for Real-Time Control of Synthesis and Compositional Algorithms" , Proceedings of ICMC, 1992.
[Lee&Wessel 93] M. Lee & D. Wessel, "Real-Time Neuro-Fuzzy Systems for Adaptive Control of Musical Processes", Proceedings of ICMC 1993.
[McAulay&Quatieri 86] R.J. Mc Aulay and Th. F. Quatieri, "Speech analysis/synthesis based on a sinusoidal representation", IEEE Trans. on Acoust., Speech and Signal Proc., vol ASSP-34, pp. 744-754, 1986.
[Nawab&Quatieri 88], S. H. Nawab and Th. F. Quatieri, "Short-Time Fourier Transform" in Advanced Topics in Signal Processing, J. S. Lim, A. V. Oppenheim Editors, Prentice-Hall, 1988.
[Nicholl 93] M. Nicholl, "Good Vibrations", Invention and Technology, Spring 1993, American Heritage.
[Peevers 93] A. Peevers. "A 3D Editor for Interactive Sound Analysis/Synthesis", CNMAT Internal Report, May 93.
[Puckette&Zicarelli 90] M. Puckette and D. Zicarelli, "MAX - An Interactive Graphic Programming Environment", Opcode Systems, Menlo Park, CA, 1990.
[Sandell&Martens 92] G. J. Sandell & W. L. Martens , 1992, "Prototyping and Interpolation for Multiple Musical Timbres Using Principal Component-Based Synthesis", Proceedings of the ICMC, 1992, CMA, San Francisco, CA.
[Serra 86] X. Serra, "A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition", PhD dissertation, Stanford Univ., 1986.
[Smith&Cook 92] J. O. Smith and P. R. Cook, "The Second-Order Digital Waveguide Oscillator," Proc. ICMC, Computer Music Association, 1992.
[Tierney et al. 71] J. Tierney, C. M. Rader, and B. Gold, "A digital frequency synthesizer," IEEE Trans. Audio Electroacoustics, vol AU-19, pp 48-57, March 1971.