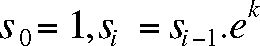 computes
computes
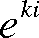 for real
and complex values of k, we can introduce these new classes to optimize
computation of exponentials and sinusoids respectively:
for real
and complex values of k, we can introduce these new classes to optimize
computation of exponentials and sinusoids respectively:Adrian Freed and Amar Chaudhary
CNMAT, 1750 Arch Street. Berkeley, CA 94709
(510) 643 9990, {adrian,amar}@cnmat.berkeley.edu
Object-oriented programming using C++ classes is established practice in the general programming community and is beginning in computer music applications. However, large components of computer music systems are still commonly written in the C programming language, either because object-orientation is felt unnecessary or more often because of efficiency concerns. Such concerns are central to successful implementations of reactive performance-oriented computer music systems. By judicious use of new features of the recently established ISO Standard C++ , real-time computer music applications may be developed that are more efficient and reliable than typical C programs, easier to understand and write, and easier to optimize for a particular operating environment. This paper reviews new features of ISO C++ relevant to reactive music system programming and illustrates by example a new programming style for musical applications that exploits unique strengths of C++.
The recently completed standardization effort for C++ was not a formal codification of existing practice with the language. Many years of the effort involved the introduction of entirely new features many of which directly address efficiency issues that have prevented C++ from use in reactive music software. Section 2 summarizes these new features and hints at their relevance to reactive music systems. References to particular sections of a readable description of the standard C++ language are offered since space limitations prevent a complete exposition of each new feature.
We are developing a new programming system for musical applications, the "Open Sound System" (OSS). We have rejected the approach of simply translating an existing library of primitives or building C++ wrappers around one of the C-based music languages for two reasons. Firstly, these legacy systems were designed for computer architectures very different from those in use today. In modern computers arithmetic is much faster than table indexing. The key to good performance these days is exploitation of parallelism, data and code locality and the multi-level register/primary/secondary/main memory hierarchy . The second reason to start from scratch is that by exploring the rich abstraction facilities of standard C++, we have identified a promising new approach for developing musical signal processing and synthesis applications that is fundamentally different from the traditional unit generator/wiring model. Section 3 illustrates this new approach by example.
The C++ standard library now includes many features specifically designed for numerical programming which is required in the signal-processing component of computer music applications.
2.1.1 Complex numbers (Stroustrup 1997) 22.5
Complex variables of single, double and quadruple precision are supported with the full range of mathematical functions.
2.1.2 Valarray (Stroustrup 1997) 22.4"Valarrays" are a low-level building block for floating point vectors and are optimized for performance. May apply aggressive optimization strategies on valarray arithmetic. "Valarray" data accesses and layout may be matched to according to algorithm access patterns, optimizing use of the memory hierarchy.
2.1.3 Limits (Stroustrup 1997) 22.2There is now a standard way of asking for properties of the built-in numeric types such as the maximum and minimum values representable in variables of a particular type.
Overloading the function call operator allows for explicit support in C++ of functors or "function objects". Functors are a natural choice for implementing unit generators and are very efficient since their calls can be "inlined", eliminating subroutine call overhead and optimizing register and data cache use.
It is common practice to use C++’s "operator overloading" feature to define matrix and vector operations resulting in high-level, compact, representations of signal processing algorithms. Unfortunately, the obvious way to do this results in horribly inefficient code with redundant creation of temporary objects for each vector operator. The solution to this problem is to use compile-time analysis and closure objects to transfer evaluation of sub-expressions into an object that implements a composite operation eliminating the call by value that creates temporaries. These "composition closure objects" may be used to expose parallelism that can be exploited by good compilers to generate optimal code sequences on modern, highly concurrent processor architectures.
2.4 Templates (Stroustrup 1997) 13 and Template Metaprograms (VeldHuizen 1996)Templates are used for implementing polymorphic types in C++. Because template functions may be "inlined" they don’t incur the run-time overhead of virtual functions, C++’s other mechanism for polymorphism.
Template metaprograms exploit the computation engine required to implement standard C++’s template mechanism for compile-time computations. includes examples that may have application in signal processing algorithms.
Standard C++ "allocators" offer the programmer explicit control over how memory is allocated and freed on a per-object basis. For OSS we have experimented with shared, garbage collected and pre-allocated pools to achieve low latency memory management and improve cache hit rates.
The new C++ exception mechanism can be used to manage unforeseen conditions in reactive systems without complete failure that would be disastrous in live musical performance.
The unit generator wiring paradigm pervades non real-time and reactive music programming software . In this paradigm, users assemble systems bottom-up from a large library of primitives. The approach described here is top-down from a high-level description of the desired function, through a series of refinements resulting in an efficient implementation.
The impulse response of a second-order resonator system is e-ktsin2¹ft. We wish to compute a suitable approximation of this function as part of an implementation of the resonance synthesis model . The "literal translation" of the continuous-time representation above into C++ is :
double damped_sine(double frequency, double amplitude, double rate, Time &t) {
return amplitude * exp(-rate*t) * sin(2.0*PI*frequency*t);
}
The following fragment will test this function for ten seconds:
for(Time t;t<10.0;++t)
cout<< damped_sine(440.0, 1.0, 0.1, t)<<endl;
This implementation of the Time iterator class implements regular sampling at a default rate of 44100kHz:
class Time {
double time; const double sampling_interval;
public:
Time(double srate=44100.0): time(0.0),sampling_interval(1.0/srate) {}
operator double() { return time; }
friend double operator *(double f, Time &t){ return f * t.time; }
Time& operator ++() { time += sampling_interval; return *this; }
};
The above implementation has the virtue of simplicity, but is too slow for real-time work since the library exponential and sine functions are computed for every sample point. The usual way to address this deficiency is to replace calls to the mathematical functions with calls to low-level optimized functions. We prefer another approach where we evolve the Time class to include formal descriptions of the mathematical identities behind the optimizations, leaving the compiler to deal with the details of exploiting the identities for the particular machine the code will run on.
The first step is to change the time representation to more honestly reflect that we are really computing discrete-time sequences:
class Time {
int sample_count; const double sampling_interval;
public:
Time(double srate=44100.0):sample_count(0), sampling_interval(1.0/srate) {}
operator double() { return sample_count*sampling_interval; }
friend double operator *(double f, Time &t) {
return f * t.sample_count*t.sampling_interval;
}
Time& operator ++() { ++sample_count; return *this; }
};
Noting that the sequence 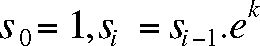 computes
computes
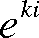 for real
and complex values of k, we can introduce these new classes to optimize
computation of exponentials and sinusoids respectively:
for real
and complex values of k, we can introduce these new classes to optimize
computation of exponentials and sinusoids respectively:
class expstate {
double value, factor;
public:
double exp(double k, int i) {
return (i==0)? (factor = ::exp(k), value=1.0) :
(value *= factor) ;
}
};
class sinstate {
complex<double> value, factor;
public:
double sin(double k, int i) {
return (i==0) ?
(factor = ::exp(complex<double>(0.0,k)), value=1.0) :
imag(value *= factor);
}
};
For the compiler to use these optimization classes, we have to specify when they may substitute for sub-expressions involving exponential and sinusoid functions. We first use a composition closure object (defmul below) to defer multiplication of double constants and time variables. Then we can define exponential and sinusoid functions that operate on defmul objects:
class Time {
private:
mutable int sample_count;
const double sampling_interval;
mutable int expindex, sinindex;
class expstate {
mutable double value, factor;
public:
double exp(double k, int i) const{
return (i==0) ? (factor = ::exp(k), value=1.0) :
(value *= factor);
}
};
vector<expstate> expstates;
class sinstate {
mutable complex<double> value, factor;
public:
double sin(double k, int i) const {
return (i==0) ?
(factor = ::exp(complex<double>(0.0,k)), value=1.0) :
imag(value *= factor);
}
};
vector<sinstate> sinstates;
public:
Time (double srate=44100.0, int depth=MAXDEPTH):
sampling_interval(1.0/srate), sinstates(depth),expstates(depth),
expindex(0),sinindex(0), sample_count(0) {}
operator double() const {
return double(sample_count) *sampling_interval;
}
const Time& operator ++() const {
expindex=sinindex=0; ++sample_count; return *this;
}
struct defmul{ // deferred multiplication
const Time& t;
const double& f;
defmul(const Time& at, const double& af): t(at), f(af){}
operator double() { return f * double(t); }
};
friend defmul operator *(const double f, const Time &t) { return defmul(t,f);}
friend defmul operator *(const Time &t, const double f) { return defmul(t,f);}
friend double exp(const defmul &dm) {
return dm.t.expstates[dm.t.expindex++].exp(
dm.f*dm.t.sampling_interval, dm.t.sample_count);
}
friend double sin(const defmul &dm) {
return dm.t.sinstates[dm.t.sinindex++].sin(
dm.f*dm.t.sampling_interval, dm.t.sample_count);
}
};
We compiled the above classes with several commercial C++ compilers. They all correctly interpreted the composition closure technique. Careful adjustment of optimization options is required to encourage compilers to "inline" implicit functions resulting from the composition closure. One notable compiler (http://www.kai.com) reasoned correctly that the complex and real exponentiation would only be computed once and that the arguments were known at compile time and thereby avoided compiling any calls to mathematical functions.
The optimization effort above did not involve changing the original function describing the computation required. This suggests that we could build a system where users define their needs in an expressive high-level form similar to a mathematical description. These descriptions would be compiled efficiently enough to run in real-time given a large enough family of optimization classes. Optimizations expressed in this form are available to the compiler as it compiles an entire application. By contrast optimized library functions are bound at the last moment by a linker program that does not have enough information to effectively exploit available computing resources. We are also encouraged by the fact that the optimizations themselves are expressed in a high-level form similar to a mathematical description making them easier to develop and debug.
Becker, P. (1998). C++ standard approved. C/C++ Users Journal. 16: 89.
Chaudhary, A. (1998). Band-Limited Simulation of Analog Synthesizer Modules by Additive Synthesis. AES 104th Convention, San Francisco, CA, AES.
Chaudhary, A., A. Freed, et al. (1998). OpenSoundEdit: An Interactive Visualization and Editing Framework for Timbral Resources. International Computer Music Conference, Ann, Arbor, Michigan.
Dowd, K. and M. K. Loukides (1993). High performance computing. Sebastopol, CA, O'Reilly & Associates.
Freed, A. (1994). Codevelopment of user interface, control and digital signal processing with the HTM environment. 5th International Conference on Signal Processing Applications and Technology, Dallas, TX, USA, DSP Associates.
Pope, S. T. (1993). "Machine tongues. XV. Three packages for software sound synthesis." Computer Music Journal 17(2): 23-54.
Potard, Y., P.-F. Baisnée, et al. (1986). Experimenting with Models of Resonance Produced by a New Technique for the Analysis of Impulsive Sounds. International Computer Music Conference, La Haye, CMA.
Stevens, A. (1998). "A C++ standard at last." Dr. Dobb's Journal 23(2): 115-17, 130-1.
Stroustrup, B. (1995). Standardization in The design and evolution of C++. ed. Reading, Mass., Addison-Wesley. 134-179.
Stroustrup, B. (1997). The C++ Programming Language. Reading, Mass., Addison-Wesley.
VeldHuizen, T. (1996). Using C++ Template Metaprograms in C++ Gems. ed. S. B. Lippman. New York, SIGS Books & Multimedia. 459-487.
Veldhuizen, T. and K. Pannambalam (1996). "Linear algebra with C++ template metaprograms." Dr. Dobb's Journal 21(8): 38, 40-2, 44.
Zicarelli, D. (1998). MSP. http://www.cycling74.com.