Matthew Wright & David Wessel
({matt,
wessel}@cnmat.berkeley.edu)
Center for New Music and Audio Technologies, 1750 Arch Street, Berkeley, CA
94709, USA
We have created a computer-based improvisation environment for generating rhythmic structures based on the concept of tal from North Indian classical music.
This work was motivated by the desire to improvise musically in collaboration with musicians trained in the North Indian (also known as "Hindustani" or "Indo-Pakistani") classical tradition [Khan 91, Jairazbhoy 95]. The goal was not to mimic the style or sound of the tabla accompaniment that is traditionally part of this genre, but rather to create a musical common ground, where computer-based rhythmic processes can generate material in response to realtime control within a framework with which the Hindustani improviser is comfortable. Our goal was to create an environment with the following characteristics:
Therefore, our design of this system began with an attempt to understand tal, the formalized theory and practice of rhythm from this music. The brief explanation of tal in this paper is based on our very slight knowledge of an ancient and richly developed tradition and should in no way be taken as definitive.
Tal is based on repeating fixed-length cycles, e.g., tin tal with 16 beats and jap tal with 12 beats. A particular tal is characterized not only by its number of beats, but also by traditional thekas, fixed patterns that would normally be played on a tabla drum to delineate the rhythmic structure of the tal in the most straightforward way. There is a language of bols, syllables which onomatapoeiacally correspond to the various tones that can be produced with tablas, e.g., "dha," "dhin," "ke," etc. These bols can be concatenated into a multisyllabic word, e.g., "tete" or "terekita," indicating multiple subdivided notes in the space of a single beat.
Tal is much more than a set of "canned" patterns to be played by a tabla player. This music is improvised by both the tabla player and the melodic singer(s) or instrumentalist(s), so the fixed patterns are more of a referent and learning aid than a mini-score to be repeated verbatim throughout a performance. (On the other hand, there do exist "electric tabla boxes," meant primarily as practice tools — essentially drum machines that repeat these theka patterns indefinitely with control of tempo and tuning [AACM].)
Tal carries rhythmic information that defines a structural framework for the improvisation. The first beat of a tal has the name sam, meaning "equal." Sam has a special significance as the resolution point for ambiguous or highly syncopated rhythms and as the ending point for musical phrases. A characteristic rhythmic idiom of this style is a melodic phrase which becomes increasingly complex near the end of a tal cycle and resolves on sam, followed by a beat or two of silence, and then the beginning of a new phrase around beat three or four of the next cycle. A tabla player might support this gesture with increasingly syncopated or complex playing at the end of the previous cycle, then a clear and strong note on sam, followed by silence or a very simple pattern at the beginning of the next cycle.
Another special beat in a tal cycle is called khali, meaning "empty." The khali beat typically comes halfway through the tal cycle, i.e., halfway between two sams. There is a tradition of clapping the important beats of a tal cycle; in fact, "tal" means "clap." Khali, however, is shown not with a clap but with a silent wave of the hand. Musically, the significance of khali is to provide a space or emptiness that contrasts and supports the strong sam beat. It is common for a theka pattern to consist of tabla tones that ring and sustain through the non-khali beats, and then muted, non-sustaining tones from khali to the next important beat.
Our work focuses primarily on tin tal, literally "three claps," which has sixteen beats. The sixteen beats are divided into four groups of four; the three claps are on beat 1 (sam), beat 5 (the beginning of the second group of 4), and beat 13 (the beginning of the last group of four). Beat 9 is khali.
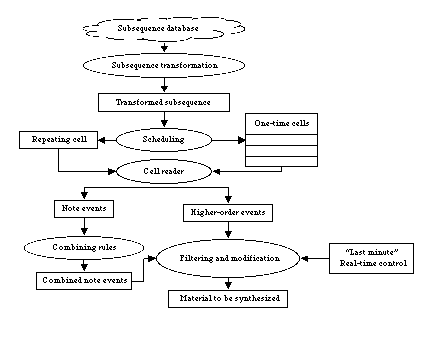
Our environment provides numerous controls for selecting, layering, scheduling, filtering, altering, and orchestrating rhythmic material. With so many points of control, it's important to have a conceptual model of the parts of the system and how they interact with each other. This section gives a model of our system, showing the various points of control and how they interact. The entire model is shown in Figure 1, using the convention that rectangular boxes represent data and circular shapes represent processes. The various ways we have attached gestural controllers to this model are beyond the scope of this short paper and described elsewhere in these proceedings [Wessel 98].

Figure 1: Overview of the entire model
Our work is based on the CNMAT Rhythm Engine (CRE), which uses CNMAT's novel representation for rhythmic structure [Iyer 97]. The important aspects of this representation for our tal work are tatums, "temporal atoms," representing the smallest cognitively meaningful subdivision of the main beat, beats, the tatums that correspond to the beats of our tal cycles, and cells, collections of beats and other tatums that represent the span of time taken by one tal cycle.
Cells store events that are associated with an instant or a span of time within that represented by the cell. The most obvious kind of event to put in a cell is a note; this is the model for programming most commercial drum machines. Our system extends this concept by providing subsequences, groups of notes or other events in some rhythmic relationship to each other. We go into a performance with a database of predefined sequences ranging from a single note to a complex rhythm lasting for many beats.
Rhythms of subsequences are defined in terms of their own beats and sub-beat tatums; the ratio between subsequence beats and beats of the current tal is determined when subsequences are scheduled to be played. A subsequence has a reference tatum, typically the tatum of the earliest note, that provides a single handle that lets the time-scaled subsequence be placed at a certain tatum in the cell. Notes in a subsequence before the reference tatum can be used to represent "pick-up" notes.
This subsequence database gives us the advantages of having a repertoire of predetermined rhythmic material available. The ability to modify subsequences and schedule them at arbitrary time points makes them much more flexible than the traditional library of preprogrammed drum sequences. By representing traditional theka patterns as subsequences, we can play each one "straight" by scheduling it on the first beat of a cycle with no time scaling, or we can use it as an ingredient for complex rhythms built during a performance.
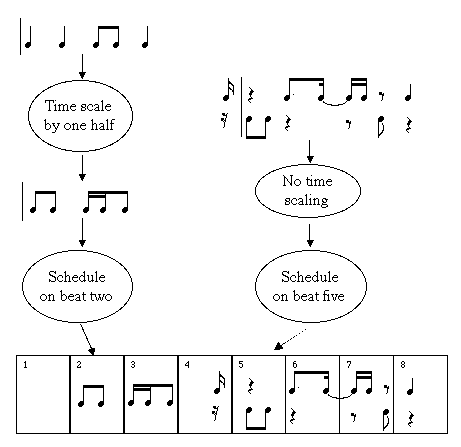
Figure 2: selection, time scaling, and scheduling of two subsequences
Figure 2 shows this process of selecting a subsequence, time scaling it, and scheduling it with respect to its reference tatum on a certain beat of a cell. The bar-line-like line shows the reference tatum of each subsequence. In the example on the left a rhythm is time scaled to be faster by a factor of two, and then scheduled on beat two of the 8-beat cell. On the right, a rhythm in two voices is scheduled on beat five of the cell. The interpretation of two-voice rhythms is determined by the orchestration controls that will be described below.
Our model uses two kinds of cells. Repeating cells hold material that is repeated on each tal cycle. It's important for the user interface to have convenient ways to remove material from repeating cells as well as put it in. One-time cells hold events scheduled at a particular tal cycle in the future. The number of one-time cells determines how far in the future events may be scheduled. The "earliest" one-time cell is for the current cycle, and therefore includes beats that have already been played. So, for example, if it's beat 13 at a certain moment, scheduling an event at beat 5 of the current cell is too late, so the event will not be played. At the end of each cycle, all of the events in this current cell have been played. The contents of the one-time cells "advance" by one cell at these cycle boundaries, so that the events that used to be scheduled for n cycles in the future become scheduled for n-1 cycles in the future.
A process called the "cell reader" continually reads events for the current tatum out of the repeating and future cells. This process happens slightly before the exact time of the tatum, not only to allow time for the subsequent processing of these events, but also to allow for temporal deviations that may place certain events ahead of the tatum.
When there are multiple notes to be played on a single tatum, there is the possibility of combining the notes in some musically meaningful way. The default behavior is not to combine: simply play all of the notes at the same time on that tatum. One interesting combining rule involves a limb abstraction, which can play only one note per tatum. When there are two notes that would have to be played at the same time by a single limb, the system combines them, e.g., by increasing the volume of one note and dropping the other. Another combining rule is automatic flamming: when two notes are to be played on the same tatum, their onset times are moved apart from each other by an amount in the 1-40 ms range. One of the perceptual consequences of flamming is the prevention of fusion and the maintenance of individual voice identity.
Some events span a fixed period of time; these are scheduled by indicating their start and end times. We have integrated a real-time sampler/looper with our rhythmic environment that allows us to capture a segment of audio in real-time and then play it back later. This works with "start record" and "end record" messages that are scheduled like any other kind of event in our system, thus allowing rhythmic precision in our sampled loops. We construct subsequences consisting of some notes followed by a "start record," followed by a "stop record"; we think of the notes before the "start record" as a musical stimulus, and then use the recording feature to capture a co-improvisor's response to this stimulus.
We have a model of rolls, series of notes played so quickly that they leave the domain of perception of individual events and instead become a composite gesture over time, with real-time manual control of volume and note density. Our rolls begin with a note on a particular tatum and "resolve" with a final note that is played precisely on another tatum; thus rolls are scheduled by indicating the tatums of their first and last notes.
We have used this rhythmic environment in conjunction with the CAST synthesizer to resynthesize a musical phrase with real-time control of time stretching and various timbral controls. The "target" feature of CAST's time machine (http://www.CNMAT.Berkeley.EDU/CAST/Server/timemachine.html#targetfeature) allows the user to schedule the resynthesis of a phrase to reach a given point at a given time in the future, while still allowing real-time control of time modification in the interim. This is another example of an event specified by scheduling its beginning and end.
Higher order events determine whether and how notes will be played. Examples include density control and crescendi and decrescendi. Our current density control mechanism is based on probabilistic masks, which define a probability for eliminating a note on each tatum. This allows, for example, the elimination all notes on non-beat tatums during a certain period. Volume controls include gradual changes like crescendi and also per-beat adjustments like "make all notes on sam stronger." Another higher order event modifies timbres or note types, which allows for controls like "don’t play any ringing notes between beats 9 and 12." In addition to being scheduled as higher order events, these kinds of controls can also be made in real-time, affecting pre-scheduled notes "at the last minute." A favorite technique is "dipping," where there is a dense stream of material scheduled and we use real-time volume or density control to keep everything silent except when a real-time gesture allows the material through for a period of time.
All event types are treated uniformly by the system, and it is straightforward to extend the system by adding new event types.
In commercial drum machines, the selection of timbres for each note is generally fixed; a pattern is defined in terms of the rhythm to be played with each timbre. We find this to be too constricting and have designed a system where the orchestration, or assignment of notes to particular timbres, can be determined and changed during performance. At the same time, as seen in Figure 1, our subsequences are defined in terms of polyphonic voices.
Our solution is to map all percussive timbres onto a single axis, basically sorting them by spectral centroid. At one end of the scale are the deepest, lowest sounds, through to the highest, brightest sounds at the other end. We define our subsequences in terms of seven abstract drum timbres along this axis named "doom," "boom," "pow," "pop," "tock," "tick," and "tsit." When we synthesize the percussion, e.g., with resonance models, this centroid is a synthesis parameter. When we use sample playback, we arrange our samples along this axis and use lookup strategies. We then provide an interface for associating particular timbres with each of the abstract names in our subsequenes.
We have used this environment in a live concert improvisation in collaboration with classically trained Indo-Pakistani musicians [Wessel 98] and found it to be expressive and powerful. It succeeded in providing a rhythmic framework that made sense both to the computer musicians and the classical. We continue to refine the system and find new ways to control it.
[AACM] Electric tabla boxes and a vast array of Indian instruments, recordings, etc., are available through the Ali Akbar College of Music Store, 215 West End Avenue, San Rafael, CA 94901, (415) 454-0581.
[Iyer 97] Iyer, V., J. Bilmes, M. Wright, and D. Wessel, A Novel Representation for Rhythmic Structure, Proc. ICMC 1997, Thessaloniki, Hellas.
[Jairazbhoy 95] Jairazbhoy, N. A., The Rags of North Indian Music, Their Structure and Evolution, Popular Prakashan, Bombay, India, 1995.
[Khan 91] Khan, A. A., and G. Ruckert, The Classical Music of North India: The Music of the Baba Allauddin Gharana as taught by Ali Akbar Khan, Volume 1, East Bay Books, distributed by MMB music, Saint Louis, Missouri, 1991.
[Wessel 98] Wessel, D., M. Wright, and S. A. Khan, Preparation for Improvised Performance in Collaboration with a Khyal Singer, Proc. ICMC 1998, Ann Arbor, Michigan.