|
Center for New Music and Audio Technologies |



Next: Implementation of various CORDIC
Up: Computing the Sine Function
Previous: Computing the Sine Function
The CORDIC-Algorithm for Computing a Sine
In 1959 Jack E. Volder [7] described the COordinate
Rotation DIgital Computer or CORDIC for the calculation of
trigonometric functions, multiplication, division and conversion
between binary and mixed radix number systems. The CORDIC-algorithm
provides an iterative method of performing vector rotations by
arbitrary angles using only shifts and adds. Volder's algorithm is
derived from the general equations for vector rotation. If
a vector 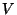 with components
with components 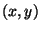 is to be rotated through an angle
is to be rotated through an angle
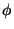 a new vector
a new vector 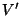 with components
with components 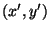 is
formed by:
is
formed by:
![$\displaystyle V'=\left[\begin{array}{c} x'\\ y'\end{array}\right]=\left[\begin...
...s(\phi)-y\cdot\sin(\phi)\\ y\cdot\cos(\phi)+x\cdot\sin(\phi)\end{array}\right]$](img8.gif) |
(1.2) |
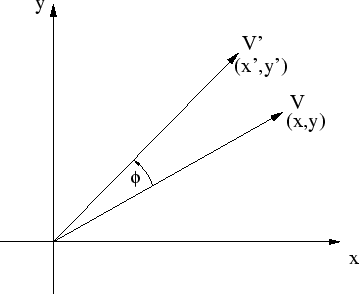
Figure 1.2 illustrates the rotation of a vector
![$ V=\left[\begin{array}{c}x\\ y\end{array}\right]$](img9.gif) by
the angle
by
the angle
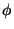 .
.
Figure 1.2:
Rotation of a vector V by the angle 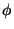
 |
The individual equations for 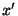 and
and 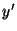 can be rewritten as [8]:
can be rewritten as [8]:
and rearranged so that:
The multiplication by the tangent term can be avoided if the rotation
angles and therefore
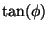 are restricted
so that
are restricted
so that
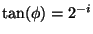 . In digital hardware
this denotes a simple shift operation. Furthermore, if those rotations
are performed iteratively and in both directions every value of
. In digital hardware
this denotes a simple shift operation. Furthermore, if those rotations
are performed iteratively and in both directions every value of
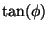 is representable. With
is representable. With
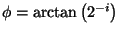 the cosine
term could also be simplified and since
the cosine
term could also be simplified and since
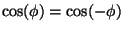 it is a constant for a
fixed number of iterations. This iterative rotation can now be
expressed as:
it is a constant for a
fixed number of iterations. This iterative rotation can now be
expressed as:
where
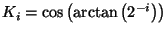 and
and
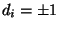 . The product of the
. The product of the
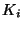 's represents the so-called K factor [9]:
's represents the so-called K factor [9]:
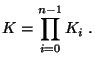 |
(1.9) |
This 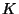 factor can be calculated in advance and applied elsewhere in
the system. A good way to implement the
factor can be calculated in advance and applied elsewhere in
the system. A good way to implement the 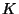 factor is to initialize the
iterative rotation with a vector of length
factor is to initialize the
iterative rotation with a vector of length  which compensates the gain inherent in the CORDIC algorithm. The
resulting vector
which compensates the gain inherent in the CORDIC algorithm. The
resulting vector 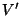 is the unit vector as shown in Figure
1.3.
is the unit vector as shown in Figure
1.3.
Figure 1.3:
Iterative vector rotation, initialized with V0
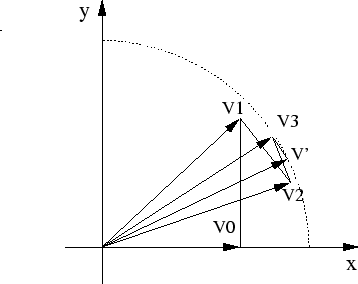 |
Equations 1.7 and 1.8 can now be simplified to the
basic CORDIC-equations:
The direction of each rotation is defined by 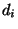 and the sequence of
all
and the sequence of
all 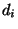 's determines the final vector. This yields to a third equation
which acts like an angle accumulator and keeps track of the angle
already rotated. Each vector
's determines the final vector. This yields to a third equation
which acts like an angle accumulator and keeps track of the angle
already rotated. Each vector 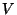 can be described by either the vector
length and angle or by its coordinates
can be described by either the vector
length and angle or by its coordinates 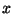 and
and 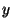 . Following this
incident, the CORDIC algorithm knows two ways of determining the
direction of rotation: the rotation mode and the vectoring
mode. Both methods initialize the angle accumulator with the desired
angle
. Following this
incident, the CORDIC algorithm knows two ways of determining the
direction of rotation: the rotation mode and the vectoring
mode. Both methods initialize the angle accumulator with the desired
angle 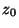 . The rotation mode, determines the right
sequence as the angle accumulator approaches 0 while the
vectoring mode minimizes the y component of the input vector1.2.
. The rotation mode, determines the right
sequence as the angle accumulator approaches 0 while the
vectoring mode minimizes the y component of the input vector1.2.
The angle accumulator is defined by:
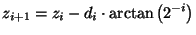 |
(1.12) |
where the sum of an infinit number of iterative rotation angles equals
the input angle 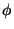 [10]:
[10]:
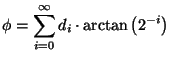 |
(1.13) |
Those values of
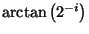 can be stored in a
small lookup table or hardwired depending on the way of
implementation. Since the decision is which direction to rotate
instead of whether to rotate or not,
can be stored in a
small lookup table or hardwired depending on the way of
implementation. Since the decision is which direction to rotate
instead of whether to rotate or not, 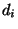 is sensitive to the sign of
is sensitive to the sign of
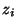 . Therefore
. Therefore 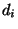 can be described as:
can be described as:
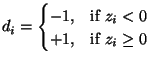 . . |
(1.14) |
With equation 1.14 the CORDIC algorithm in rotation
mode is described completely. Note, that the CORDIC method as
described performs rotations only within  and
and  . This
limitation comes from the use of
. This
limitation comes from the use of 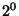 for the tangent in the first
iteration. However, since a sine wave is symmetric from quadrant to
quadrant, every sine value from 0 to
for the tangent in the first
iteration. However, since a sine wave is symmetric from quadrant to
quadrant, every sine value from 0 to 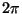 can be represented by
reflecting and/or inverting the first quadrant appropriately.
can be represented by
reflecting and/or inverting the first quadrant appropriately.



Next: Implementation of various CORDIC
Up: Computing the Sine Function
Previous: Computing the Sine Function
Home
Norbert Lindlbauer
2000-01-19
![]()
![]()
![]()
![$\displaystyle V'=\left[\begin{array}{c} x'\\ y'\end{array}\right]=\left[\begin...
...s(\phi)-y\cdot\sin(\phi)\\ y\cdot\cos(\phi)+x\cdot\sin(\phi)\end{array}\right]$](img8.gif)
![$ V=\left[\begin{array}{c}x\\ y\end{array}\right]$](img9.gif) by
the angle
by
the angle